La résolution proposée par Terzaghi, puis Taylor utilise les séries de Fourier. Les solutions vont être fonction des conditions aux limites et de la géométrie du problème.

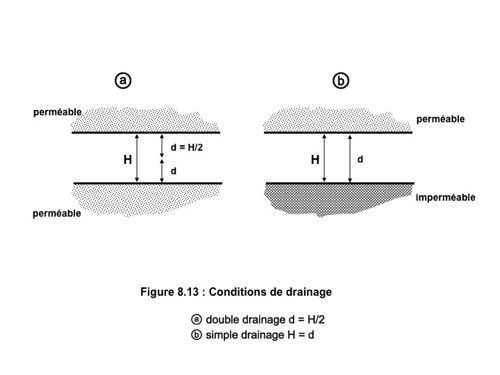
1 – Le drainage peut être simple ou double (fig. 8.13). On notera d le parcours de drainage (le plus long parcours vertical qu’une particule d’eau a à parcourir pour atteindre une frontière perméable) ; (H étant l’épaisseur de la couche) :

• si le drainage est simple d = H ;
• et si le drainage est possible au dessus et au dessous de la couche .

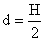2 – La forme de l’excès de pression interstitielle initiale, le cas 1 sur le graphique 8.15 est celui qui est le plus classiquement rencontré.

3 – A la fin du processus, pour t = ∞, tout l’excès de u est dissipé.

L’équation de la consolidation peut être reformulée avec des grandeurs adimensionnelles :

dans laquelle,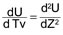

• Z = z/d profondeur relative (z étant l’altitude du point, d le parcours de drainage).
• Tv est le facteur temps  ;
• U le degré de consolidation.

La solution dans le cas unidimensionnel qui nous intéresse s’exprime de la manière suivante :

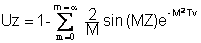avec M = (π/2) (2 m + 1)

Degré de consolidation local :

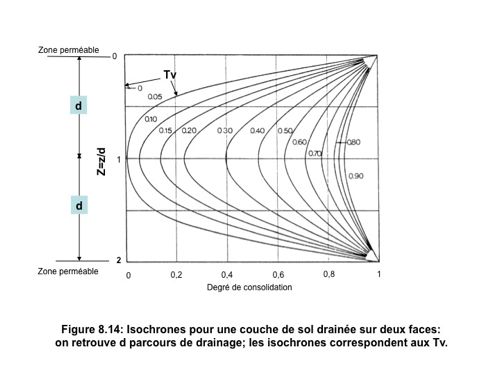
Dans le cas où le drainage est sur les 2 faces, on peut à partir de la solution dessiner des isochrones en facteur temps Tv paramétrées en Z = z/d (fig. 8.14). Ceci permet de trouver en un point quelconque de la couche le degré de consolidation local, en pression interstitielle uz, ou au contraire en gain de contrainte effective.

Lorsque Tv = 0, on est à l’état initial où la pression interstitielle est égale au supplément de contrainte totale.

Lorsque Tv = 0,05, le processus de consolidation est engagée et la pression interstitielle résiduelle a chuté à 0 aux frontières perméables, alors qu’elle est encore pratiquement égale à la valeur initiale au centre de la couche. Cette différence de pression va s’atténuer avec la croissance de Tv, le « moteur » de l’écoulement de l’eau dans la couche diminue en « puissance ».

Degré de consolidation global :

En intégrant sur toute la hauteur de la couche, et en tenant compte des valeurs locales de Uz, on obtient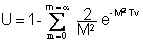

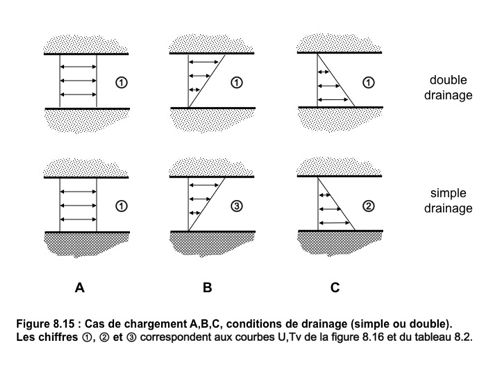
Ceci permet de relier le degré de consolidation global au facteur temps Tv par des relations établies une fois pour toutes, en fonction des conditions de chargement et de drainage définies sur la figure 8.15.

• Le cas A correspond à l’application d’une surcharge sur une surface très large par rapport à l’épaisseur de la couche considérée, ou à un rabattement de nappe ;
• Le cas B décrit ce qui correspond à l’application d’une charge sur une petite surface ;
• Le cas C est celui de la consolidation sous poids propre d’un sol constituant un remblai.

La figure 8.16 donne les relations U – Tv pour les différents cas. Pour le cas n° 1, celui qui est le plus courant, des équations approximatives permettent de calculer U en fonction de Tv dans 2 domaines :

Si U < 60 % Tv = π/4 U2 ;

Si U > 60 % Tv = 1,781 – 0,933 log (1 – U).

Les valeurs de U en fonction de Tv sont également données dans le tableau 8.2.

Tableau 8.2 – Valeurs de Tv en fonction de U pour les 3 cas