Pour prédire dans la réalité le déroulement de la consolidation et pouvoir calculer les vitesses de tassement et les tassements du sol, ou au besoin d’une théorie adaptée qui a été développée par Terzaghi. Il s’agit d’une équation différentielle inspirée des équations de la chaleur. La forme des équations qui ont été établies par Terzaghi est semblable à celles qui décrivent le refroidissement d’une barre d’acier initialement portée à une température donnée. D’une certaine manière, on peut dire que l’excès de température est analogue à l’excès de pression interstitielle et la conductivité thermique à la perméabilité du sol (plus exactement au Cv défini ci-dessous).

Cette théorie nécessite des hypothèses de base parmi lesquelles on retient en particulier :

• les déformations et les écoulements sont unidimensionnels (uniquement verticaux),
• la loi de Darcy est valide ;
• la perméabilité k et le coefficient de compressibilité volumétrique m_v sont constants dans un intervalle de charge donné ;
• les grains du sol et l’eau sont incompressibles ;
• l’absence de consolidation (compression) secondaire ;
• la surcharge est appliquée instantanément et sur toute l’épaisseur de la couche de sol.

Terzaghi étudie un petit élément de sol (fig. 8.12) et calcule pour cet élément infinitésimal le volume d’eau sortant du sol. Ce volume est fonction à la fois de la perméabilité du sol et des charges appliquées qui sont différentes à l’entrée et à la sortie de l’élément. Sur la figure 8.12, la pression interstitielle d’entrée est u, celle se sortie (u – Δu) et les charges respectivement h = u/γ_w et (h – dh) =(u - du)/γ_w , de sorte que la vitesse de sortie (v + dv) est supérieure à la vitesse d’entrée v.

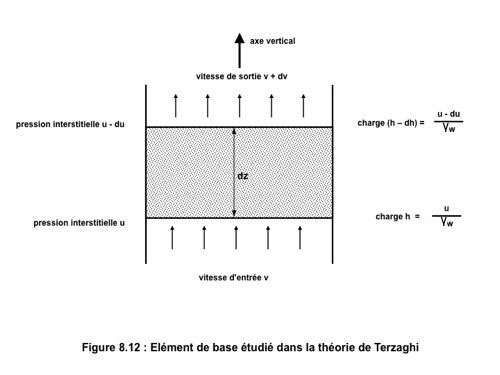
Dans l’élément, le gradient appliqué est i = dh/dz.

Le changement de volume associé à ce phénomène, pendant une période de temps dt peut s’écrire de la façon suivante : 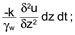, z étant la variable de profondeur.

Il faut bien noter que la pression interstitielle u dans l’élément de sol va être fonction à la fois du temps et de la profondeur.

D’un autre côté, on met en relation le changement de volume du sol (traduit par le changement d’indice des vides) et la variation de contrainte effective grâce au coefficient de compressibilité a_v défini au paragraphe 8.5.2. On a évidemment Δσ’ = -Δu, u restant à la fois fonction de z et de t.

Soit : .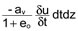

On égale les deux manières d’obtenir la variation de volume et on obtient :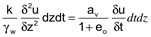

soit .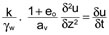

On pose 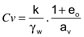et ce coefficient est appelé le coefficient de consolidation (exprimé en m²/s). On peut remarquer que C_v est décrit comme une constante, ce qui entraîne que k et a_v sont des constantes. Ceci est une approximation à peu près valide dans un faible domaine de variation des contraintes effectives. En réalité, ce n’est pas le cas, puisque k va diminuer avec la diminution de e et que av va également décroître.

L’équation de consolidation unidimensionnelle s’écrit alors :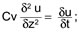

sa résolution permettra de déterminer en fonction du temps t et de la position dans la couche z, la valeur de la pression interstitielle résiduelle u_t.

Connaissant u_t à une profondeur et un instant donné, on peut alors définir un degré de consolidation local U_z = 1-u_t/u₀, u₀ étant la valeur initiale de la surpression générée par le chargement.

On regarde maintenant l’ensemble de la couche et on s’intéresse aux tassements de cette couche en fonction du temps. Soit S_f le tassement final (lorsque toute la suppression interstitielle s’est dissipée) ; en notant S_t le tassement de la couche à l’instant t, on définit un degré de consolidation global U = S_t/S_f, U égale 0 au début du processus et vaut 1 à la fin.

Plusieurs méthodes existent pour la résolution de l’équation de la consolidation, certaines sont mathématiquement exactes, d’autres ne sont qu’approximatives.