Considérons la figure A.5. Nous avons tout d’abord le plan réel (fig A.5.a) autour d’un point M pour lequel on connait par exemple les contraintes principales σ₁ et σ₃. On construit dans le plan de Mohr (fig. A.5.b) le cercle de diamètre σ₁, σ₃. Puis fictivement, on lie les deux plans dans une position fixée, ceci permettra de passer d’un plan à l’autre.

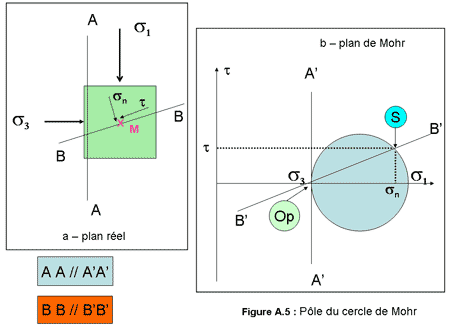
On considère dans le plan réel la droite AA qui correspond à l’orientation sur laquelle s’exerce σ₃, puis on trace dans le plan de Mohr la parallèle  A’A’ à AA passant par le point du cercle où la valeur de la contrainte est σ₃.
A’A’ recoupe le cercle de Mohr en un point généralement distinct du point représentant la contrainte de départ, ce point est nommé O_p pôle du cercle de Mohr (Ici cas particulier A’A’ est tangent au cercle).

Si l’on veut connaître maintenant la valeur de la contrainte s’exerçant sur la direction BB dans le plan réel, il suffit de tracer B’B’ passant par O_p et le point S d’intersection avec le cercle de Mohr donne par son abscisse et son ordonnée les valeurs respectives de σ_n et de τ.
 
Noter que si l’on prend une direction perpendiculaire à BB, on obtient dans le cercle de Mohr un point diamétralement opposé à S, c’est-à-dire une valeur de contrainte normale différente et une valeur de contrainte tangentielle égale à la précédente en valeur absolue et de signe opposé.

On retiendra que lorsqu’une facette tourne d’un angle θ dans le plan réel, le point représentatif du vecteur contrainte dans le plan de Mohr tourne de 2θ