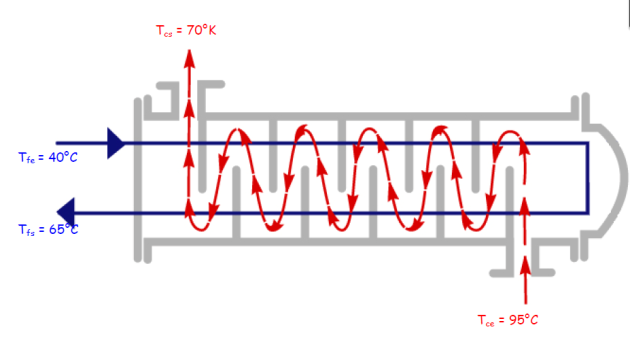
Exercice 3
Calculez les aires d’échange nécessaires pour diverses configurations afin d’effectuer l’échange ci-dessous :
Question
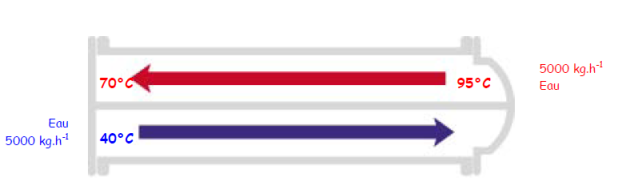
Le coefficient de transfert H est évalué à 2325 W.m-2.K-1. les arrangements choisis sont les suivants : contre courant, co-courant, une passe calandre et 2 passes tubes.
Indice
On commencera par calculer le flux de chaleur échangé dans l’appareil, ainsi que la température de sortie du fluide froid. On en déduit alors la Différence de Température Moyenne Logarithmique ΔTml pour une configuration contre-courant.
Ensuite, pour chaque configuration envisagée, on pourra lire le facteur F dans les graphes 5 à 8, et en déduire, par application de la relation (19) la surface d’échange nécessaire.
Résultat
1. On commence par calculer la puissance thermique échangée dans l’installation. A partir de l’égalité des flux de chaleur échangés (relation (1)), on en déduit la température de sortie du fluide froid.
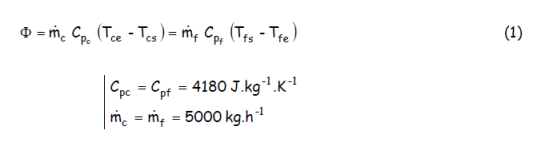
d’où :

2. Surface de l’échangeur à contre-courant
On commence par calculer la Différence de Température Moyenne Logarithmique ΔTml pour une configuration contre-courant.
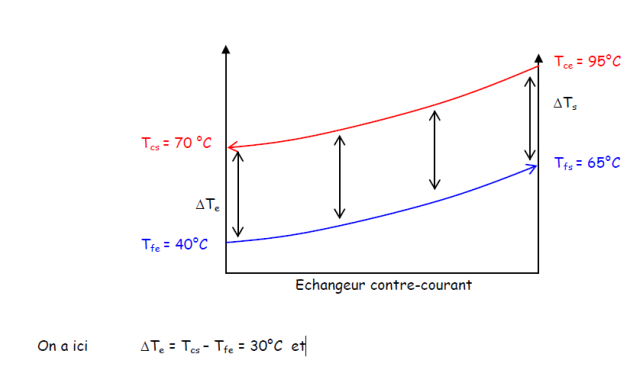
ΔTs = Tce – Tfs = 30°C
d’où une impossibilité de calcul pour la Différence de Température Moyenne Logarithmique ΔTml (on trouve 0/0).
En fait, ce cas assez rare est généralement observé lorsque les débits et capacités calorifiques des deux fluides sont identiques. Toute la chaleur perdue par le fluide chaud sur un élément de longueur dx est gagnée par le fluide froid. Les débits et capacité calorifiques étant identiques, on a donc, pour ce cas particulier une différence de température entre fluides chaud et froid constante le long de l’échangeur et égale à ΔTe ou ΔTs :
ΔTml_contre-courant = ΔTe = ΔTs.= 30°C
Par définition, le facteur correctif F est égal à 1 pour un échangeur à contre-courant.
On a donc
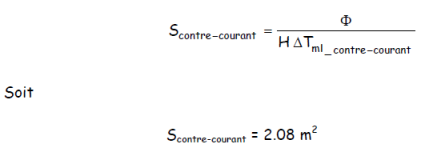
3. Surface de l’échangeur co-courant
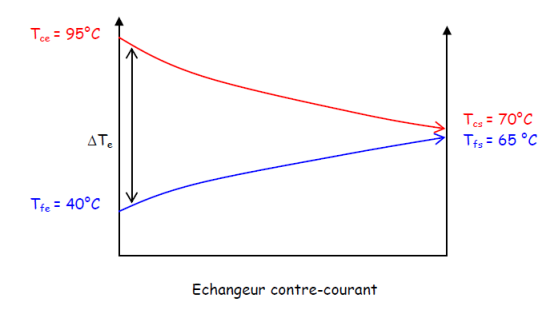
On a ici ΔTe = Tce – Tfe = 55°C et ΔTs = Tcs – Tfs = 5°C
d’où cette fois ci un calcul aisé de la ΔTml :
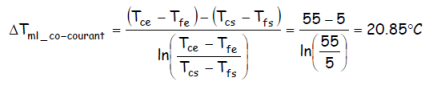
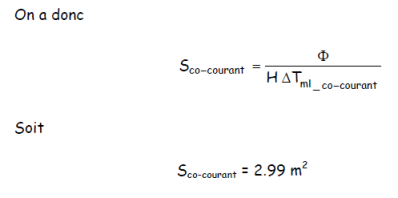
4. Surface de l’échangeur à une passe calandre et deux passes tubes
Dans ce cas, il faut faire intervenir le facteur F, la ΔTml étant définie par rapport à l’échangeur contre-courant.
On sait que F dépend de :
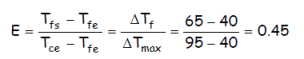
et de
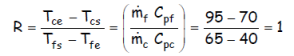
On utilise alors la figure 5, et on lit :
F≈0.88
On en déduit finalement :

5. Conclusion
On remarque que la configuration co-courant conduit à la surface d’échange la plus élevée, et que la configuration 1 passe calandre et deux passes tubes conduit à une surface d’échange légèrement supérieure à la configuration contre-courant.