Cas général (échangeur multitubulaires)
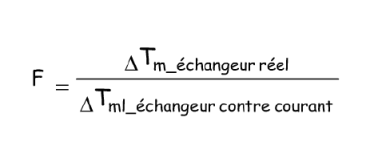
3.1 Méthode du facteur de correction F
On vient de voir que le calcul de ΔTm = ΔTml est particulièrement simple dans le cas d’un échangeur à tubes co-axiaux. Cependant cette configuration ne permet pas la réalisation d’appareils à grandes surfaces d’échange. L’extension la plus simple est l’échangeur tubes calandre à une passe calandre et deux passes tubes (figure 4).
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Notons que ce type d’échangeur peut être utilisé lorsque de grandes vitesses de circulation sont nécessaires pour accroître le coefficient de transfert à la paroi interne des tubes. Ceci pourrait être justement réalisé, à partir d’un échangeur à une seule passe de tubes, en doublant la longueur de l’échangeur et en divisant par deux le nombre de tubes. Il en résulterait un meilleur coefficient de transfert, ce qui se traduirait par une surface d’échange de moindre étendue. Cependant la longueur d’un échangeur est limitée en pratique par les facilités d’entretien et de réparation : le faisceau de tubes doit pouvoir s’enlever sans difficultés ; il faut également ajouter le facteur d’encombrement. Ainsi les échangeurs à passes multiples présentent-ils de l’intérêt à cause de leur compacité bien que la surface d’échangeur nécessaire soit relativement plus importante.
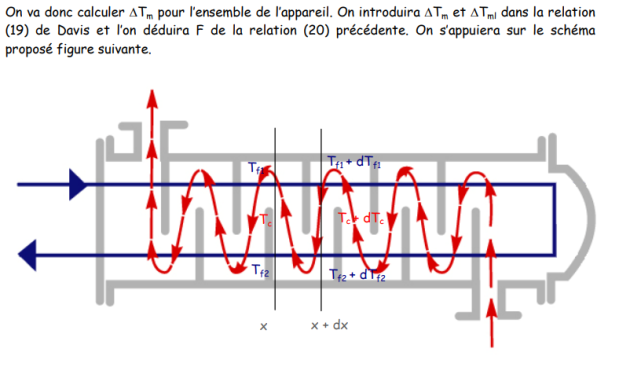
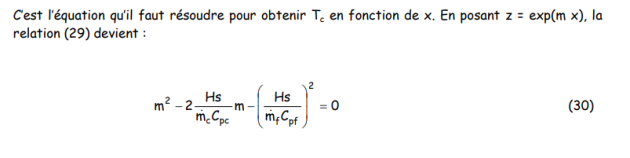
Compte tenu de la complexité qui résulte de la configuration "une passe calandre et deux passes tubes", et qui est en quelque sorte une combinaison de co-courant et contre-courant, il n’est plus possible d’utiliser la loi de Newton sous la forme de la relation (16), où ΔTml représente la différence de température moyenne logarithmique. Il faut trouver une nouvelle expression de ΔTm. En fait, dès 1931, Davis a proposé de remplacer la loi de Newton par une relation (de Davis) de la forme :
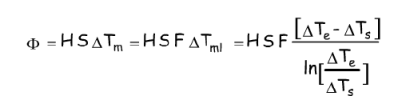
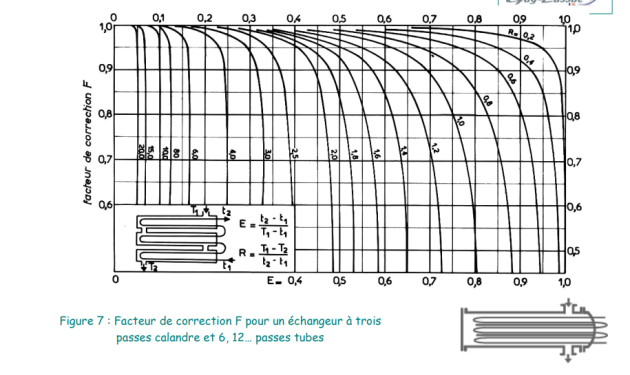
ce qui revient à multiplier la différence de température moyenne logarithmique par un facteur correctif F. Cette méthode, initialement développée pour des échangeurs à une passe calandre et deux passes tubes, a ensuite été étendue à d’autres types d’échangeurs, pour lesquels on a calculé les valeurs de F. Ces dernières sont le plus souvent représentées sous forme de graphes, et peuvent être trouvées dans de nombreux ouvrages spécialisés.





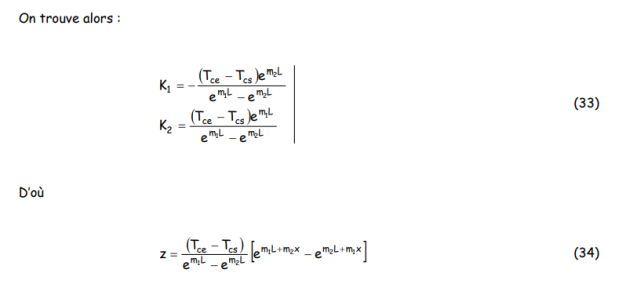





Les variables E et R ont des significations physiques simples :
• E est le rapport de l‘élévation de température du fluide froid à la différence de température des fluides chaud et froid à leur entrée dans l’appareil et peut être considéré comme un critère d’efficacité.
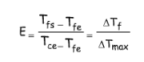
• R est le rapport de la chute de température du fluide chaud à l’élévation de température du fluide froid, et c’est aussi le rapport des capacités calorifiques de ces fluides.
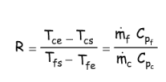
On retiendra que F est égal à un pour les échangeurs à tubes co-axiaux, il est inférieur à 1 pour les échangeurs à configuration complexe, et est aussi égal à 1 lorsque la température de l’un des fluides ne change pas (condenseur ou rebouilleur).
Pour diverses configurations, les valeurs du facteur de correction F sont indiquées ci-après :
Dans le cas d’un échangeur tubes et calandre à M passes calandre et un nombre pair de passes tubes, le calcul conduit à l’expression suivante pour le facteur de correction F :
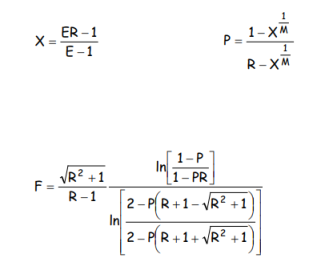
On remarquera que si M = 1 (cas d’une passe calandre) le calcul conduit à P = E, et on retrouve l’expression (46) démontrée pages précédentes.
Des figures, plus commodes à utiliser que les formules donnant les valeurs du facteur de correction F, sont présentées pages suivantes pour les mêmes configurations d’échangeurs.
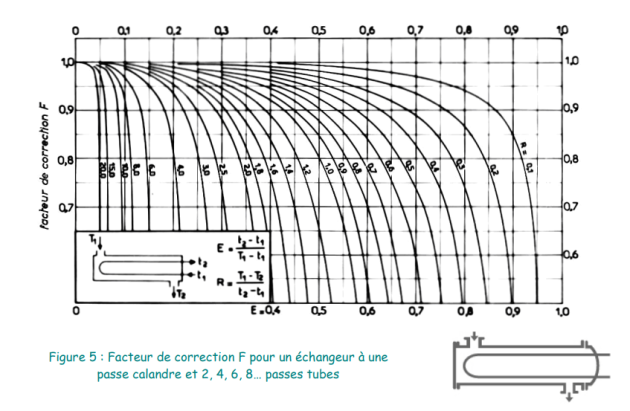
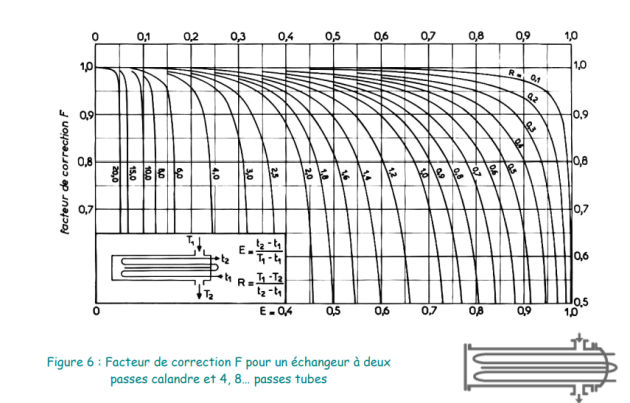
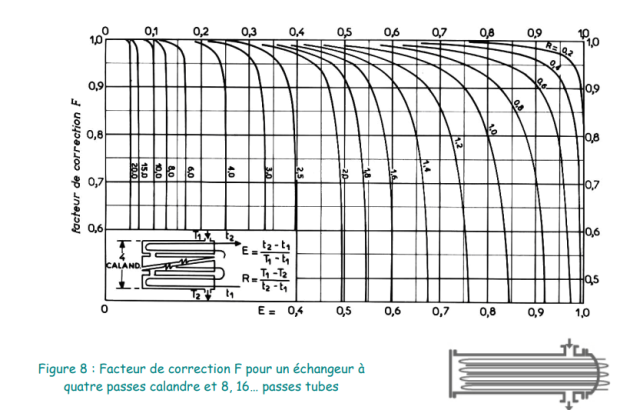
3.1 Méthode NUT
Il est simple et commode d’utiliser la méthode ∆Tml lorsque les températures d’entrée des fluides sont connues et que leurs températures de sortie sont imposées ou facilement accessibles à partir des bilans d’énergie (relation (1)).
Cependant, il arrive fréquemment que seules les températures d’entrée soient connues et que l’emploi de la méthode ∆Tml exige de procéder à un calcul par itération qui peut dans certains cas se révéler fastidieux. Il est alors préférable d’utiliser une méthode désignée sous le nom de "méthode du Nombre d’Unités de Transfert" et abrégée en "méthode NUT"
3.2.1 Efficacité de l'échangeur
On définit l’efficacité de l’échangeur par la relation :
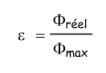
où Φmax est le flux de chaleur maximum théoriquement échangeable. Un tel transfert pourrait en principe être réalisé par un échangeur à contre-courant de dimension infinie. Dans un tel appareil, l’un des fluides subirait une différence de température maximum de (Tce – Tfe).




3.2.2 Nombre d'unité de transfert
On peut caractériser n’importe quel échangeur par le Nombre d’Unités de Transfert (NUT) défini par :

On notera que NUT est un paramètre adimensionnel, rapport du temps caractéristique de passage τ sur un temps caractéristique de transfert de chaleur. En effet, partant de la définition du NUT, on peut écrire :

3.2.3 Relations pratiques
On peut montrer que pour n’importe quel type d’échangeur il existe des relations entre ε, NUT et r, où NUT et ε ont été définis aux paragraphes précédents et r est le rapport des capacités calorifiques :

On trouve dans la littérature des abaques représentant la fonction ε=f(NUT) pour différentes valeurs de r (0 < r < 1). Les plus courantes sont présentées ci-après.
Le principe de la méthode est alors de calculer le NUT, le rapport r, d’en déduire l’efficacité ε, enfin le flux de chaleur échangé dans l’installation.


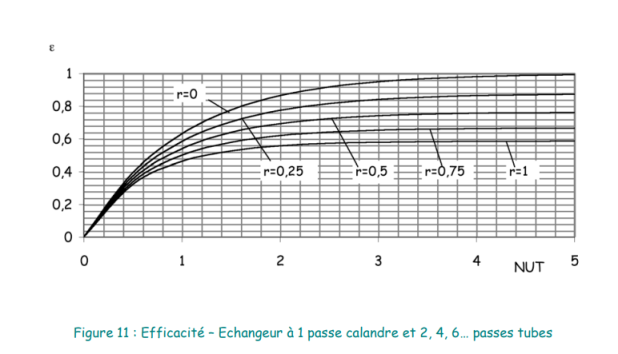
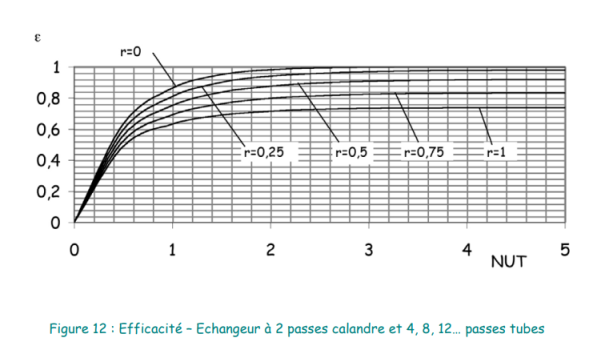
3.3 Exemples
Voir exercice 3 et 4
4.Conclusion
Les notions présentées dans ce chapitre restent essentielles pour l’étude et la compréhension du fonctionnement des échangeurs de chaleur. Elles seront complétées dans les chapitres suivants par le calcul des coefficients de transfert de chaleur disponibles dans les différentes configurations, mais il faudra à chaque fois estimer le coefficient de transfert de chaleur nécessaire par les relations générales présentées ci-dessus.
REMARQUE : Particulièrement, l’ingénieur de Génie des Procédés sera confronté à deux grands types de problèmes : l’utilisation d’un échangeur existant ou le dimensionnement d’un nouvel appareil.
4.1. Utilisation d'un échangeur existant
La démarche proposée est alors la suivante :
• Calcul du coefficient global de transfert de chaleur Hnécessaire à partir du flux de chaleur échangé dans l’installation et de la Différence de Température Moyenne Logarithmique :
• Calcul du coefficient de transfert de chaleur disponible dans l’installation Hdisponible à partir de la configuration de l’échangeur, des caractéristiques physico-chimiques des fluides et des coefficients de film hc et hf (voir les chapitres suivants pour leurs calculs).
• Si Hdisponible est supérieur au Hnécessaire, alors l’échangeur est utilisable. Dans le cas contraire (Hdisponible inférieur à Hnécessaire) l’échangeur proposé ne convient pas, et il faut s’orienter vers un autre appareil, ou modifier les conditions de fonctionnement (changement de débit, de température d’entrée …).
4.2 Dimensionnement
La démarche proposée est alors :
• Définir les paramètres de fonctionnement (nature des fluides, températures et pression, débits...),
• Choisir une configuration d’échangeur (contre-courant, tubes calandre, échangeur à plaques...).
• Cette configuration étant choisie, on se ramène au cas précédent. C’est à dire qu’on commence par déterminer le coefficient global de transfert de chaleur nécessaire Hnécessaire à partir du flux de chaleur échangé dans l’installation et de la Différence de Température Moyenne Logarithmique :
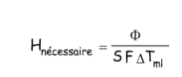
• On calcule ensuite le coefficient de transfert de chaleur disponible dans l’installation Hdisponible à partir de la configuration de l’échangeur, des caractéristiques physicochimiques des fluides et des coefficients de film hc et hf (voir les chapitres suivants pour leurs calculs).
• On joue ensuite sur la géométrie de l’échangeur (longueur ou diamètre des tubes pour un simple contre courant, nombre de passes, nombre, diamètres ou longueur de tubes… pour un tubes calandre, taille et nombre de plaques pour un échangeur à plaques…) de façon à avoir un coefficient de transfert de chaleur disponible légèrement supérieur au coefficient de transfert de chaleur nécessaire, et une perte de charge acceptable dans l’installation.
4.3 Conclusion
Cette vidéo synthétique reprend les principaux points abordés au cours de ce chapitre.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Nous verrons au cours des chapitres suivants comment ces notions générales s’appliquent à des cas plus particuliers.
Le chapitre 2a est consacré au fonctionnement et dimensionnement des échangeurs tubescalandre. Le chapitre 2b concerne les échangeurs à plaques, les chapitres 2c et 2d les condenseurs et rebouilleurs ou évaporateurs. Enfin, le chapitre 2e concerne le transfert de chaleur dans les réacteurs agités. À chaque fois, un exercice d’application permettra d’illustrer les notions abordées.
Nous recommandons au minimum la lecture et la réalisation des exercices des chapitres 2a et 2b, afin que le lecteur ait de bonnes connaissances générales sur le dimensionnement des principaux appareils d’échange de chaleur. Les chapitres suivants concernent des cas plus particuliers, mais toutefois fréquemment rencontrés dans l’industrie (notamment le transfert de chaleur dans les réacteurs agités, omniprésents en chimie fine). Une simple lecture permettra déjà au lecteur de se familiariser avec le fonctionnement et le dimensionnement des principales installations.