Diffraction de Bragg
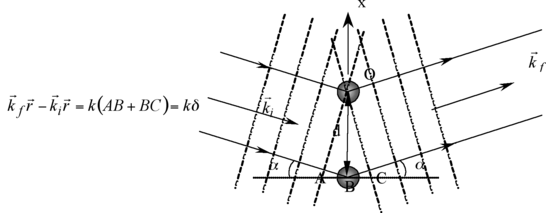
Le but de cet exercice est de retrouver la relation de diffraction dite de Bragg. Cette relation est similaire à la relation des réseaux que vous avez vu en optique. Ici, la relation est générale, en ce sens qu’elle est aussi valable pour des particules massiques. On reproduit l’expérience des fentes d’Young, mais cette fois les fentes sont remplacées par deux atomes, jouant le rôle de centres diffuseurs, espacés d’une distance réticulaire d. Le flux de particules arrive sur le matériau selon un angle α par rapport à la médiane de l’axe définie par les deux atomes, et on examine le faisceau diffusé selon le même angle en sortie. Comme en optique, on associe une fonction mathématique à chaque particule, caractéristique d’une onde plane :
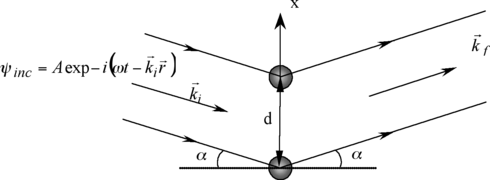
L’onde diffusée par un atome est sphérique. Néanmoins, le détecteur de particules étant à une très grande distance des atomes comparée à la distance réticulaire, l’onde diffusée arrivant sur le détecteur peut être considérée comme une onde plane en excellente approximation. Comme pour les fentes d’Young, on se propose de calculer l’amplitude puis l’intensité de l’onde diffusée.