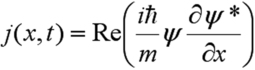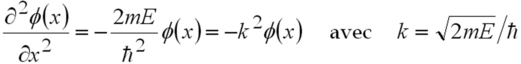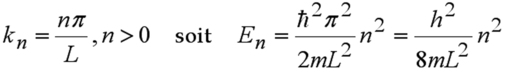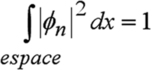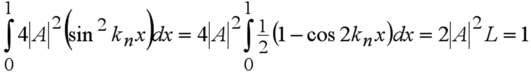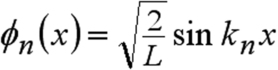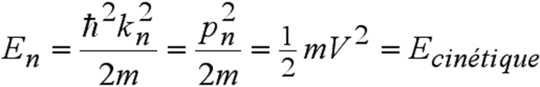Physique Quantique : de la base aux nouvelles technologies
CoursOutils transverses
Puits de potentiel infini
Nous nous proposons d'examiner les solutions de l'équation de Schrödinger stationnaire dans le cas d'une particule enfermée dans une boîte de taille L. On se place à une dimension et le potentiel est considéré comme nul dans la boîte, infini à l'extérieur.