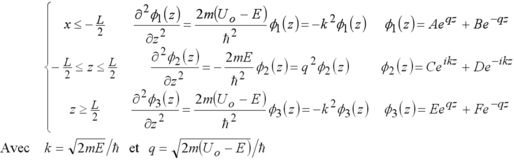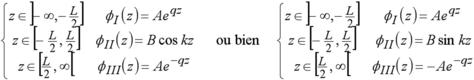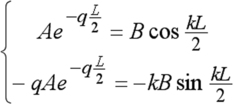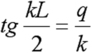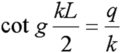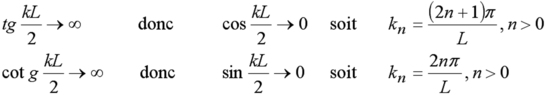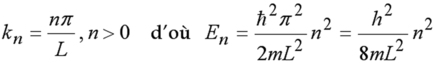Physique Quantique : de la base aux nouvelles technologies
CoursOutils transverses
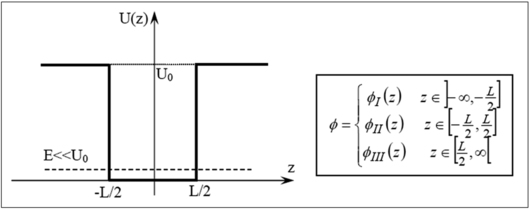
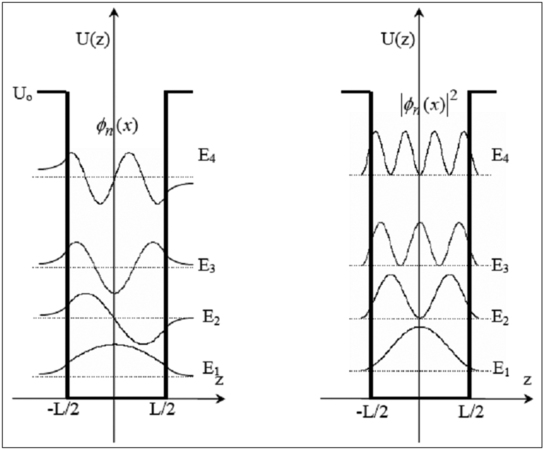
Puits de potentiel fini
Nous reprenons l'exercice précédent mais cette fois pour un potentiel fini. Le potentiel est pris égal à zéro dans le puits de largeur L et égal à U0 à l'extérieur. Soit une fonction d'onde
![]() décrivant un état stationnaire d'énergie E.
décrivant un état stationnaire d'énergie E.