Condensation d'une vapeur pure
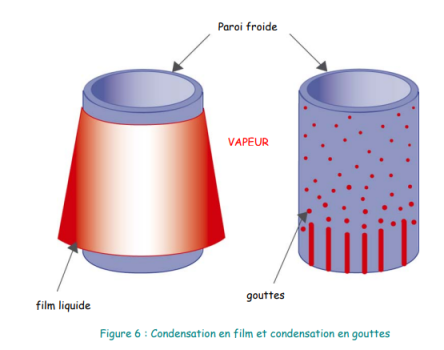
Lorsque la vapeur se condense sur une paroi froide, on peut observer une condensation en film (filmwise condensation) ou une condensation en gouttes (dropwise condensation) (voir figure 6) :
- La condensation en film est le phénomène le plus fréquemment rencontré. Le condensat forme ici un film liquide continu qui recouvre la paroi froide et qui s’écoule sous l’action des forces de gravité. C’est ce film liquide, interposé entre la vapeur et la paroi froide, qui limitera les transferts de chaleur et qui donc fixera la valeur du coefficient de transfert de chaleur.
- La condensation en gouttes apparaît lorsque la paroi froide est mal mouillée par la vapeur. Des microgouttes se forment en différents endroits de la surface (site de nucléation), puis grossissent, coalescent, et forment finalement des rigoles, qui s’écoulent le long de la paroi sous l’action de la gravité. Dans le cas de la condensation en gouttes, une large partie de la surface de refroidissement est recouverte d’une couche liquide extrêmement fine, de résistance thermique négligeable, et le coefficient de transfert de chaleur est alors beaucoup plus élevé qu’en condensation en film.
Toutefois, l’apparition de la condensation en gouttes dépend essentiellement de la mouillabilité de la paroi par la vapeur à condenser. Elle nécessite soit un traitement de surface (coûteux) soit l’ajout d’un promoteur (délicat, car risque de contamination), elle est donc très rarement rencontrée dans les équipements industriels.
Nous nous limiterons donc ici à la description de la condensation en film.
3.1. Coefficient de film a la condensation a l'extérieur des tubes
3.1.1. Tubes verticaux
On se limite pour commencer au cas d’un écoulement laminaire, c’est-à-dire pour lequel le nombre de Reynolds est inférieur à 2100.
Soit Af mc la section de l'anneau de condensat autour du tube de longueur L et le débit massique de vapeur (voir figure 6). On peut définir un diamètre équivalent par :
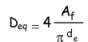
Avec Nt le nombre de tubes du faisceau, on peut définir un débit massique GV de condensat par unité de longueur de périmètre de tube :
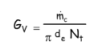
Ainsi que la vitesse massique de condensat G par :
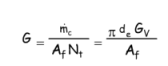
L'expression du nombre de Reynolds dans le film de condensat devient :
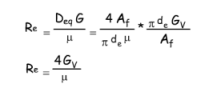
On peut alors montrer, en se basant sur les équations de transfert de chaleur en régime laminaire (cf. Perry’s, Wuithier, Kreith & Bohn, Hewitt) que le coefficient de film dépend du nombre de Reynolds, à une puissance négative, et des caractéristiques physico-chimiques du film liquide de vapeur condensé (estimées à la température du film, voir plus loin) :
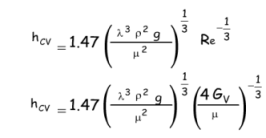
3.1.2. Tubes horizontaux
On peut définir, pour des tubes horizontaux et toujours pour des nombres de Reynolds inférieurs à 2100, un débit de condensat GH par unité de longueur de tube :
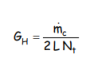
On obtient une expression analogue pour le coefficient local de transfert de chaleur, qui dépend toujours du Reynolds avec un exposant négatif, ainsi que des propriétés physico-chimiques du film liquide :
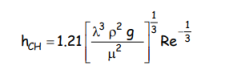
Soit
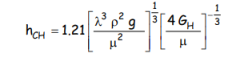
Cette dernière relation ne tient pas compte des interactions entre tubes horizontaux : en effet, le condensat ruisselle d’un tube sur l’autre, ce qui modifie le transfert de chaleur, et l’on doit alors diviser le coefficient global par 4 1 Nt , ce qui revient à définir GH par la relation suivante :
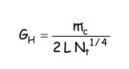
3.1.3. Régime turbulent
Les relations (5) et (7) ci-dessus ont été établies à partir de relations uniquement valables en régime laminaire.
Des nombres de Reynolds supérieurs à 2100 sont très rarement atteints, sur des tubes horizontaux, de sorte que la relation (7) n’a pas été extrapolée.
Pour des tubes verticaux, on peut utiliser la relation suivante dans le cas de nombres de Reynolds supérieurs à 2100 :
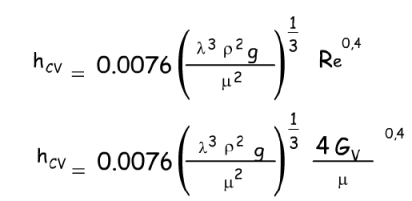
3.2. Coefficients de film a la condensation a l'intérieur des tubes
Les corrélations sont ici beaucoup moins précises et beaucoup plus rares.
3.2.1. Tubes verticaux
Nous proposons toutefois, pour de la condensation à l’intérieur d’un tube vertical, la relation suivante :
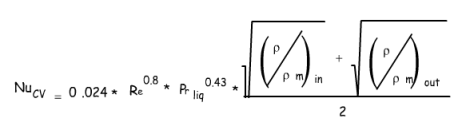
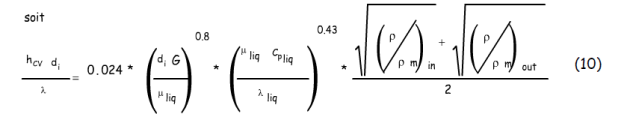
avec :

et x le titre massique du fluide diphasique en écoulement dans le tube, calculé à partir des débits partiels de fluide toujours sous forme vapeur, vapcm, et de fluide déjà condensé, liqcm, soit :
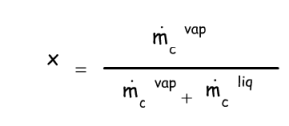
3.2.2. Tubes horizontaux
Enfin, pour des tubes horizontaux, on pourra utiliser la relation suivante :
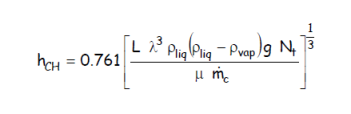
où L est la longueur des tubes, et les caractéristiques physico-chimiques sont évaluées à température de film.
3.3. Calcul d'un condenseur
3.3.1. Relations générales
La condensation d'une vapeur pure s'effectue à température constante Tc, la température de saturation de la vapeur. Toutes les configurations d’échangeurs conduisent à la même différence de température, et le facteur de correction F est donc égal à 1, quelque soit le condenseur.
On a donc :

Si l'on appelle hi le coefficient de film interne relatif au fluide de réfrigération, he le coefficient de film à la condensation, et λm la résistance due à l’épaisseur du tube, l'expression du coefficient global de transfert H disponible côté externe ou interne sera :
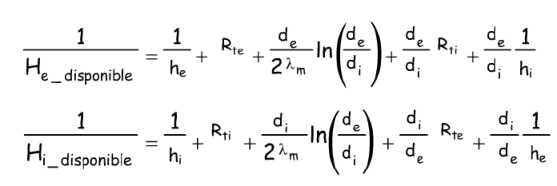
où Rte et Rti sont les résistances d’encrassement intérieur et extérieur.
3.3.2. Température de film
Par ailleurs, il convient, pour le calcul de Hdisponible, d’évaluer le coefficient à la condensation he à partir des caractéristiques physico-chimiques du liquide, à la température de film Tfilm.
Les températures moyennes des fluides chauds et froids peuvent aisément être calculées par :
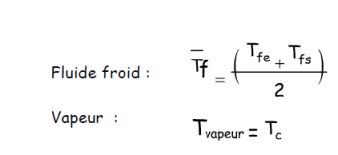
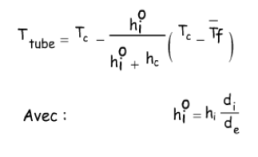
En écrivant la conservation du flux de chaleur, la température de paroi du tube est donnée par :
Et la température du film liquide Tfilm pour laquelle on calcule λ, μ et ρ est enfin donnée par :
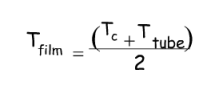
Et l'on prendra bien évidemment soin de vérifier que Hdisponible >= Hnécessaire
3.3.3. Perte de charge
Le calcul de la perte de charge côté vapeur est relativement délicat. La perte de charge est généralement estimée en prenant la moitié de la valeur calculée pour le débit total de vapeur dans les conditions d’entrée. On se basera donc sur la relation (3) proposée au chapitre 2a :
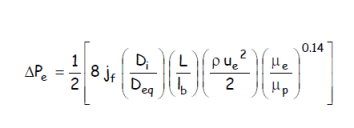
où le facteur de frottement jf est lu sur la figure 9.2 du chapitre 2a, rappelée ci-dessous.
Il conviendra toujours de vérifier, après démarrage de l’installation, que la perte de charge côté vapeur n’entraîne pas de modification du débit condensé.
La perte de charge relative au fluide de réfrigération sera estimée de la même façon que pour les échangeurs de chaleur (par exemple, par la méthode de Kern - cf. partie 2a)
