Méthodologie
Méthode d'analyse de sensibilité
L'analyse de sensibilité des résultats de l'ACV aux valeurs des grandeurs d'entrée a pour objectif d'identifier les paramètres ou grandeurs qui ont la plus forte influence sur l'un ou l'autre des indicateurs d'impacts. Ce sont ces données qu'il faut connaître avec le plus de précision pour minimiser l'incertitude sur les déterminations des indicateurs d'impact. L'analyse de sensibilité identifiera également les données d'entrée de moindre sensibilité qui n'ont que peu d'influence sur le calcul d'impact et pour lesquelles une valeur approximative ou un ordre de grandeur peut être suffisant.
La connaissance des données ou paramètres à forte sensibilité guidera aussi la recherche de solutions techniques pour réduire les charges environnementales du produit étudié.
L'analyse de sensibilité monoparamétrique évalue la sensibilité d'un résultat calculé à chacune des données d'entrée. Chaque valeur de paramètre d'entrée xi est modifiée tour à tour d'une même variation relative Δxi/xi . Le simulateur calcule la nouvelle valeur de l'impact Ij pour cette valeur modifiée de xi. La valeur trouvée de Ij est utilisée pour calculer la variation ΔIj par rapport à la valeur initiale de Ij et sa variation relative ΔIj/Ij.
L'indicateur de sensibilité Sji de l'impact Ij à ce paramètre xi est calculé comme le rapport des variations relatives grandeurs de sortie et d'entrée :
-
Sji = ΔIj/Ij / Δxi/xi (7.1)
Méthode de l'analyse d'incertitude
L'analyse d'incertitude a pour objectif d'évaluer l'incertitude ou la variabilité des résultats de l'ACV compte tenu de l'incertitude ou de la variabilité des grandeurs d'entrée. La connaissance de l'incertitude sur les résultats de l'évaluation permet de définir l'intervalle de confiance pour les valeurs calculées des différents indicateurs d'impact. L'analyse d'incertitude est notamment indispensable dans le cas d'une étude d'ACV comparative pour pouvoir conclure si la différence entre deux scénarios est significative ou non.
Concernant les grandeurs d'entrée, l'analyse d'incertitude prend en compte :
-
les variabilités sur certaines données. Ce sont par exemple, les variations des rendements de culture, des compositions des plantes ou des intrants utilisés selon les régions de production ou les années
-
les incertitudes sur des données les plus difficilement accessibles, comme par exemple les consommations d'énergie électrique des opérations unitaires ou les données ACV des intrants énergétiques et chimiques. Dans un premier temps, il est conseillé de prendre un ordre de grandeur pour ces données, ce qui implique une incertitude relativement élevée. Si la présente analyse montre une forte contribution de certaines de ces données sur l'incertitude des indicateurs d'impact, une recherche bibliographique plus approfondie devra être réalisée pour préciser les valeurs de données
L'incertitude sur la valeur d'un indicateur d'impact dépend à la fois de l'incertitude ou variabilité des valeurs de tous les paramètres ou grandeurs qui ont une influence sur cet indicateur et des sensibilités de l'indicateur par rapport à ces paramètres. La méthodologie utilisée est celle de la propagation des incertitudes couramment utilisée en métrologie. Elle consiste dans un premier temps, à évaluer les incertitudes des grandeurs d'entrée, puis à utiliser les facteurs de sensibilité Sji précédemment déterminés pour calculer les contributions individuelles des paramètres d'entrée à l'incertitude sur les indicateurs d'impact, enfin à combiner l'ensemble de ces contributions pour l'obtention d'une incertitude globale.
L'analyse d'incertitude portera sur deux indicateurs d'impact : l'indicateur IPEC de la consommation d'énergie primaire en MJ/kg éthanol et l'indicateur IGWP de potentiel de réchauffement global ou d'émission de gaz à effet de serre en kg CO2/kg éthanol, les deux grandeurs étant déterminées par la méthode d'allocation par substitution.
Caractérisation de l'incertitude ou de la variabilité des grandeurs d'entrée
Une grandeur d'entrée de valeur xi est caractérisée par une incertitude ou une variabilité U(xi), et un domaine de variation [xi - U(xi), xi + U(xi)]. On définit aussi l'incertitude ou la variabilité relative U(xi) / xi
La méthode de propagation des incertitudes associe à chaque grandeur d'entrée une probabilité de distribution de la valeur dans le domaine de variation ou d'incertitude sous la forme d'une loi de distribution. Les lois les plus utilisées sont :
-
la loi de distribution normale ou gaussienne, caractérisée par une valeur moyenne et un écart type décrivant la variation autour de la moyenne
-
la loi de distribution triangulaire caractérisée par une valeur centrale qui a la plus forte probabilité et des valeurs minimales et maximales ayant une probabilité nulle
-
la loi de distribution rectangulaire caractérisée par une probabilité identique pour toutes les valeurs dans le domaine de variation de la grandeur d'entrée
Le choix de la loi de distribution permet le calcul de l'incertitude-type u(xi) qui correspond à un écart type de la distribution. L'incertitude-type u(xi) est calculée à partir de l'incertitude U(xi) par l'une des relations suivantes :
-
pour une distribution normale
u(xi) = U(xi)/3 = 0,33 U(xi) (7.2)
supposant un intervalle de confiance à 99 % pour la valeur de xi
ou u(xi) = U(xi)/2 = 0,5 U(xi) (7.3)
supposant un intervalle de confiance à 95 % pour la valeur de xi
-
pour une distribution triangulaire
Form7-4 | (7.4) |
-
pour une distribution rectangulaire
Form7-5 | (7.5) |
Calcul de l'incertitude-type de l'indicateur d'impact
La méthode de propagation des incertitudes vise à caractériser la distribution des valeurs d'un indicateur d'impact Ij par une valeur moyenne et un écart type. Pour un indicateur d'impact Ij qui dépend d'un ensemble de valeurs xi de paramètres d'entrée indépendants, l'incertitude-type u(Ij) est donnée par la loi de propagation :
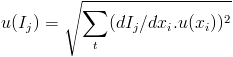 Form7-6 | (7.6) |
La dérivée dIj/dxi peut être exprimée en fonction des indicateurs de sensibilité Sji précédemment définis :
dIj /dxi = (dIj/Ij) / (dxi/xi) . Ij / xi = Sji . Ij / xi (7.7)
On peut aussi introduire la grandeur u(Ij,xi) définie par la relation :
u(Ij,xi) = dIj/dxi . u(xi) (7.8)
Elle représente la contribution individuelle du paramètre xi sur l'incertitude globale de l'indicateur Ij. Avec cette notation l'incertitude-type globale u(Ij) pour Ij est donnée par la relation :
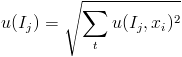 Form7-9 | (7.9) |
Evaluation de l'incertitude élargie de l'indicateur d'impact
Connaissant l'incertitude-type u(Ij) pour l'impact Ij, on peut calculer une incertitude élargie U(Ij) caractérisant l'intervalle de confiance de la valeur calculée de Ij par la relation :
Form7-10 | (7.10) |
avec k défini comme le coefficient d'élargissement. Sur la base d'une distribution normale de la valeur de Ij, le coefficient d'élargissement est pris égal à 2 pour un intervalle de confiance Ij-U(Ij), Ij+U(Ij) à 95%, et égal à 3 pour un intervalle de confiance à 99%. Avec cette incertitude élargie le résultat du calcul de l'indicateur d'impact I(Ij) s'écrit sous la forme :
Form7-11 | (7.11) |
