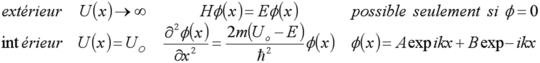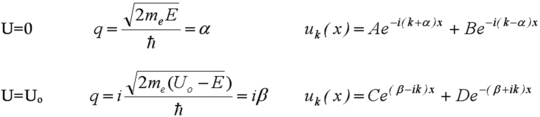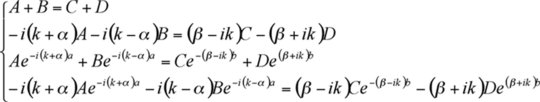3 – Application directe de la mécanique ondulatoire

En utilisant cette démarche, vous traiterez en exercices des situations simples comme le puits de potentiel ou la barrière de potentiel.

Ces exemples « académiques » que vous trouverez dans tous les livres de mécanique quantique peuvent paraître simplistes. Il n'empêche qu'ils présentent un véritable intérêt physique et pratique, sans nécessité d'outils mathématiques complexes, ce que nous allons voir par la suite.

Voir l'animation : Méthode générale en mécanique ondulatoire

Etudions dans un premier temps le cas d'une particule soumise à un puits de potentiel. C'est typiquement le cas d'un électron autour d'un noyau par exemple, sauf qu'ici nous simplifions la forme du potentiel pour rendre simple la résolution mathématique. On considère un puits de potentiel infini à une dimension (figure 11). Le potentiel (ou plus exactement l'énergie potentielle) dans le puits est considéré constant et égal à . note Le puits est de largeur . On examine les états stationnaires pour une particule de masse m tels que :

avec .

On aboutit effectivement à des solutions sinusoïdales car d'où . Les conditions aux limites de notre problème nous conduisent à obtenir des fonctions d'onde correspondant à des niveaux discrets d'énergie tels que :

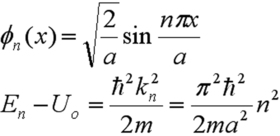
Vous avez évidemment déjà traité ce genre de problème avec la corde vibrante. Les états trouvés sont des états stationnaires (évidemment) dont la demi-longueur d'onde est un multiple de la largeur du puits, exactement comme pour la corde. Remarquez également qu'en utilisant la relation de De Broglie vous retrouvez ce que vous avez appris sur l ‘énergie à savoir :

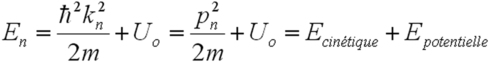
C'est la forme la plus simple de potentiel qu'on peut choisir. Elle conduit à une quantification des niveaux d'énergie comme pour des électrons autour du noyau (potentiel coulombien), ou bien des électrons libres dans un métal (potentiel constant avec barrière de potentiel en bord d'échantillon), ou encore un nucléon dans un noyau (interaction forte).

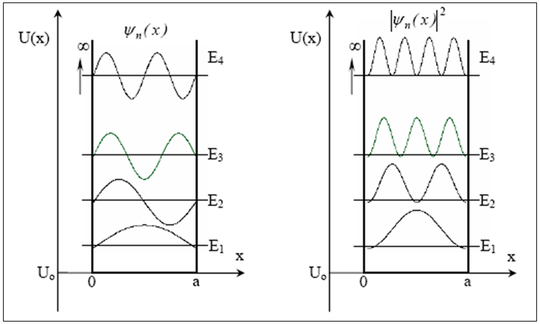
Voir l'animation : Solutions stationnaires dans un puits de potentiel infini

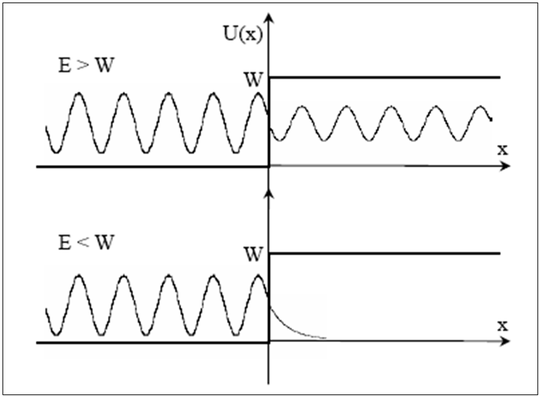
On peut traiter ce problème de façon analogue mais en considérant cette fois que le puits n'est pas infini, c'est à dire que le potentiel au bord de la boîte est fini (figure 12). L'énergie étant définie à une constante près, on choisit le potentiel nul dans la boîte et égal à W en dehors de la boîte. On examine donc les solutions stationnaires dans les deux régions, à savoir dans et hors de la boîte. Deux cas de figures se présentent. Soit l'énergie de la particule est supérieure à la barrière, et on trouve des ondes sinusoïdales stationnaires dans les deux régions (ce cas nous intéresse peu ici), soit l'énergie de la particule est inférieure à la barrière et il n'y a pas d'onde stationnaire dans la partie à fort potentiel. Le potentiel étant fini, il existe néanmoins une fonction d'onde non nulle dans cette zone qui s'atténue exponentiellement à mesure qu'on s'éloigne de l'interface entre les deux milieux. Vous calculerez en exercices ces différentes fonctions d'onde et vous trouverez que la fonction d'onde dans le milieu à fort potentiel s'écrit :

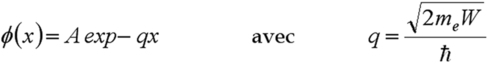
Les potentiels étant de quelques eV, q est de l'ordre du nm-1, ce qui fait que cette fonction décroît extrêmement rapidement à mesure qu'on s'éloigne de la surface.

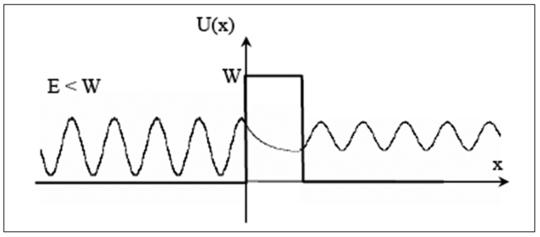
Quel est l'intérêt d'une telle étude ? Elle est en fait à la base de la microscopie tunnel. En effet, ce schéma correspond par exemple aux électrons libres dans un métal, en choisissant de la taille de l'échantillon et non de la taille de la portée du potentiel atomique. A la limite de la surface de l'échantillon, on peut modéliser l'attraction de l'électron (par les atomes de l'échantillon lui-même) par une barrière de potentiel en bord d'échantillon. Cette barrière étant finie , il existe donc une probabilité de présence non nulle en dehors de l'échantillon. Prenez maintenant une pointe métallique, qui présente également une probabilité de présence des électrons non nulle à l'extérieur près de sa surface. Approchez ainsi cette pointe près de l'échantillon, de telle sorte que les densités de probabilité de présence des électrons se recouvrent : il s'établira alors un courant appelé courant tunnel, alors même qu'il n'y a pas contact (figure 13). En effet, le vide entre la pointe et l'échantillon constitue une barrière de potentiel qui ne devrait pas être franchie si on raisonne de façon classique. En mécanique ondulatoire, c'est possible pour des particules.

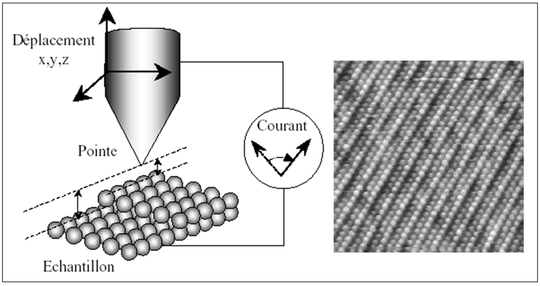
Ce courant tunnel est utilisé depuis deux décennies pour réaliser un microscope qui permet de « voir » les atomes (en fait on voit la densité électronique des couches externes). Cette technique est effectivement extrêmement sensible d'une part parce que la distance entre l'échantillon et la pointe est faible (de l'ordre du nanomètre), et d'autre part parce que le courant varie exponentiellement avec cette distance. Ainsi, la simple présence d'un plan atomique supplémentaire en surface fait passer la distance pointe échantillon de 1 nm à nm selon qu'on monte ou on descende la marche. Une telle variation de 20% de la distance provoque une variation de 200% du courant ! Ainsi, si la pointe se termine par quelques atomes, il est possible d'obtenir la résolution atomique. Un exemple d'image avec une telle résolution est donné sur la figure 14.

Voir l'animation : Microscopie à effet tunnel

Nous n'allons évidemment pas exposer toute la physique atomique ici. Nous nous proposons simplement de vous montrer les bases de cette physique construite à partir de la mécanique quantique. Nous allons traiter l'atome d'Hydrogène. Le problème se pose de la façon suivante : le système est constitué d'un noyau comportant un proton et un neutron, autour duquel « gravite » un électron. Le potentiel est de type coulombien. Le système comportant 3 particules, il faudrait résoudre le problème en considérant les coordonnées des ces 3 particules. Nous allons simplifier le problème en considérant que le noyau est immobile. L'Hamiltonien du système s'écrit ainsi comme la somme de l'énergie cinétique de l'électron et du potentiel coulombien en .

Le problème ne dépend donc que de la distance de l'électron au noyau et nous sommes ainsi ramenés en bonne approximation à un problème d'une particule dans un potentiel central. Nous sommes donc amenés à résoudre l'équation de Schrödinger indépendante du temps suivante (avec ) :

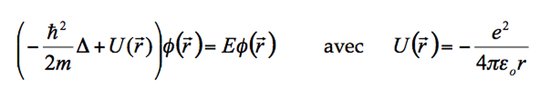
En raison de la forme du potentiel, nous pouvons traiter ce problème en symétrie sphérique pour laquelle l'opérateur s'écrit :

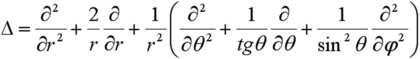
Les solutions mathématiques de ce type d'équation sont connues et s'écrivent sous la forme d'une partie appelée partie radiale, et d'une partie appelée partie orbitale (en math ces fonctions sont appelées harmoniques sphériques) :

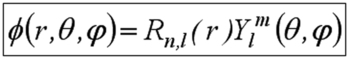
La recherche des solutions analytiques est décrite dans le fichier joint . Ce qui nous intéresse ici, c'est de faire le lien avec ce que vous avez appris auparavant. On trouve des fonctions d'onde qui dépendent de trois grandeurs n, l, m qu'on appelle nombres quantiques.

• n est dit nombre quantique principal et correspond aux couches K, L, M,... que vous avez appris.

• l est le nombre quantique azimutal : il est entier positif et prend toutes les valeurs telles que .

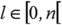• Enfin, m est dit nombre quantique magnétique : c'est un entier positif ou négatif et peut prendre toutes les valeurs telles que .

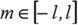Un bilan des résultats avec la forme des fonctions d'onde est donné sur le tableau suivant. Notez que ces résultats sont également valables pour des atomes n'ayant qu'un seul électron sur sa couche externe, atomes dits hydrogénoïdes.

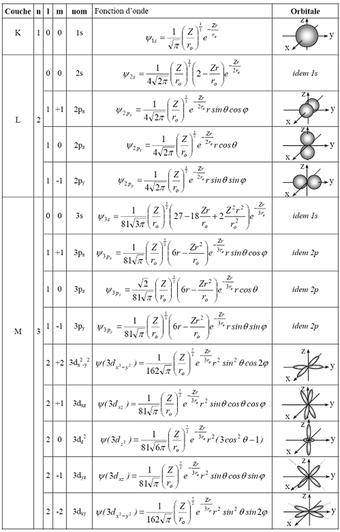
Vous pouvez télécharger ce tableau des nomenclatures sous format .PDF : Tableau sous format .PDF

Il est intéressant de considérer non plus un atome seul mais une succession d'atomes rangés selon un réseau, comme on le trouve dans la nature tout au moins pour des échantillons parfaitement ordonnés (monocristaux). Ainsi les électrons voient un potentiel périodique coulombien, qui constitue une suite de barrières de potentiel pour passer d'un atome à un autre (figure 15). Nous allons simplifier ce potentiel coulombien en un créneau pour nous ramener à ce que nous avons vu précédemment.

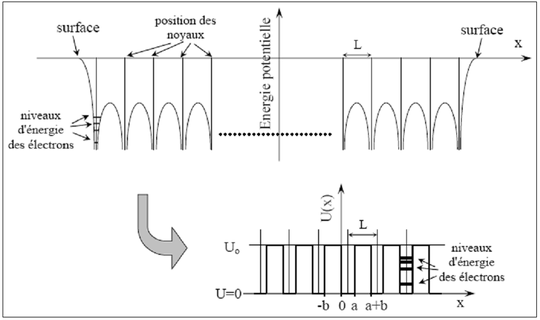
Bien évidemment, la plupart des électrons vont rester autour des noyaux, seuls les électrons de la couche externe pourront passer d'un atome à l'autre en franchissant la barrière par effet tunnel. Nous allons simplifier le problème à l'extrême en supposant que ces électrons de conduction n'interagissent pas entre eux, et que tous les noyaux et autres électrons de cœur ne sont pas perturbés. On se ramène ainsi à un problème à un électron, régi par l'équation de Schrödinger indépendante du temps avec un potentiel périodique (à 1 dimension) :

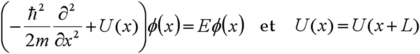
La résolution d'un tel problème a été proposée par Kronig et Penney. Tout d'abord, Floquet et Bloch ont montré que les solutions générales s'écrivent comme le produit d'une onde plane et d'une fonction qui possède la périodicité du réseau (connu sous le nom de théorème de Bloch), soit:

En injectant dans l'équation de Schrödinger, il vient :

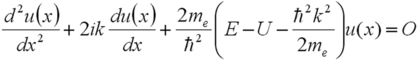
Avec U=0 pour 0<x<a, et U=Uo pour a<x<a+b. Cette équation peut s'écrire comme :

Notez que q n'est pas forcément réel. Cette équation admet pour solution générale :

Les solutions deviennent donc selon le potentiel (on rappelle que E<Uo) :

Il s'agit maintenant d'écrire les équations de continuité sur u(x) et sa dérivée (ce qui revient au même que la fonction d'onde)

en x = 0 d'une part, et en x = et x = -b d'autre part, ce qui donne :

Ce système admet des solutions non nulles seulement si le déterminant est nul soit :

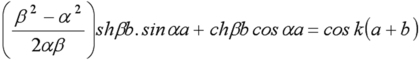
Il est possible de discuter plus simplement cette équation et de trouver les solutions en énergie en faisant tendre b vers zéro ce qui revient à considérer un potentiel avec une suite de pics de Dirac. On diminue b mais on garde l'aire du créneau constant soit :

L'équation précédente se simplifie ainsi comme :

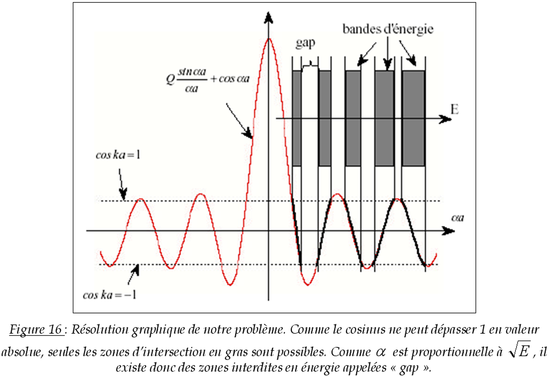
La recherche des solutions est alors graphique, en traçant les deux fonctions de part et d'autre du signe égal, et en remarquant que le cosinus est borné entre –1 et 1. Rappelez vous que ce que nous cherchons ce sont les solutions en énergie par l'intermédiaire de . On remarque ainsi graphiquement (figure 16) que ne peut pas prendre toutes les valeurs, puisqu'il existe des plages pour lesquelles l'expression précédente n'est pas satisfaite. On parle alors de bandes d'énergie séparées par des gaps.

La présence de bandes d'énergie dans la matière permet d'expliquer simplement la conduction. En effet, deux cas de figures se présentent :

1. La dernière bande (recevant les électrons de plus haute énergie) n'est pas totalement remplie, et dans ce cas les électrons peuvent se déplacer vers des niveaux vacants. Il y a conduction du courant, caractéristique des métaux. On parle de bande de conduction.

2. La dernière bande est totalement remplie (on parle de bande de valence), les électrons ne disposent plus de niveaux vacants proches en énergie et il n'y a donc pas de conduction. On parle d'isolants.

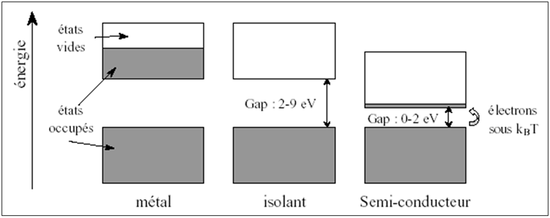
Un matériau pur et très abondant sur terre et présentant ce caractère semi-conducteur est le silicium, Si. Il est fabriqué sous forme de disque jusqu'à 30 cm de diamètre, entièrement monocristallin (l'ordre cristallographique est parfait d'un bout à l'autre du disque !). Il est à la base de l'invention du transistor (Bardeen et Britain – 1947). Les retombées technologiques de cette découverte sont énormes puisque le transistor est utilisé pour réaliser les puces électroniques présentes dans pratiquement tous nos appareils d'utilisation courante : appareils audio, vidéo, photo, ordinateurs, électroménagers, voitures...L'industrie des puces s'appelle la microélectronique. Sachez qu'un autre composé semi-conducteur est utilisé, l'arsenure de gallium, GaAs. Il est utilisé dans un appareil que nombre d'entre nous possède : le téléphone portable.

Alors, que répondrez-vous si on vous demande à quoi servent la mécanique quantique et la physique statistique ?