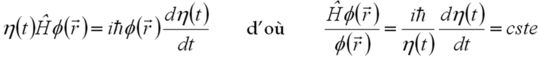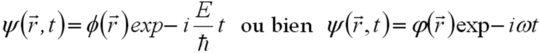2 – Fondement de la mécanique ondulatoire
Postulats de base de la mécanique ondulatoire
Nous avons ainsi tous les éléments pour construire une théorie ondulatoire de la matière. Cette théorie s'appuie donc sur 3 postulats :
-
Postulat 1 : Toute particule matérielle peut être décrite par une fonction complexe
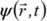 appelée fonction d'onde. Toute l'information concernant la particule à l'instant
appelée fonction d'onde. Toute l'information concernant la particule à l'instant
 et la position
et la position
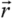 est comprise dans cette fonction.
est comprise dans cette fonction.
-
Postulat 2 : Le module carré de la fonction d'onde
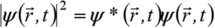 est la densité de probabilité de présence de la particule au point
est la densité de probabilité de présence de la particule au point
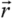 et à l'instant t.
et à l'instant t.
-
Postulat 3 : La fonction d'onde d'une particule suit l'équation d'évolution spatio-temporelle dite de Schrödinger, qui s'écrit :
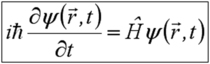
Nous disposons ainsi d'un outil mathématique qui sert à décrire l'état physique de la particule à tout instant et en tout endroit, outil appelé fonction d'onde. La signification physique de cette fonction d'onde réside dans son module carré qui donne la probabilité de trouver la particule à un instant donné à un endroit donné. Enfin, nous disposons d'une équation d'évolution qui nous permet de prédire le comportement de la particule dans le temps.
Notons que ces postulats énoncés ici pour une seule particule sont aussi valables pour une assemblée de N particules, pour laquelle on peut définir une fonction d'onde globale dépendant de toutes les coordonnées des particules et du temps. L'Hamiltonien quant à lui dépendra des coordonnées d'espace et de temps mais aussi des quantités de mouvement.
On écrira ainsi :
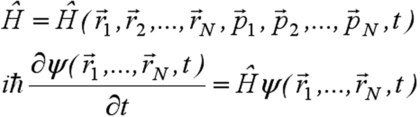
Enfin, il convient de noter un dernier point extrêmement important : l'équation de Schrödinger est une équation linéaire, ce qui implique que si l'on possède deux solutions de l'équation, alors toute combinaison linéaire de ces deux solutions est également solution. Ainsi, si on peut identifier deux fonctions d'onde correspondant à deux situations physiques différentes, toute situation physique correspondant à un « mélange « des deux situations précédentes est également possible.
A partir de cette mise au point, il convient de faire une remarque d'une grande importance pratique dans le cas de particules indépendantes. Prenons un système de 2 particules et examinons la probabilité de trouver une particule en
![]() et l'autre en
et l'autre en
![]() à l'instant t, soit :
à l'instant t, soit :
Ainsi, la fonction d'onde du système peut être écrite comme le produit de deux fonctions d'onde à variable séparée, soit :
Dans ce genre de cas l'équation de Schrödinger précédente pourra se ramener à des équations découplées ne concernant qu'une seule particule.
Etats stationnaires, équation de Schrödinger indépendante du temps
Dans le cadre de ce cours, nous ne traiterons pas de cas où l'Hamiltonien dépend du temps. Dans ce cas, l'équation de Schrödinger peut se résoudre simplement par séparation des variables en cherchant des solutions du type
![]() . Ainsi, l'équation de Schrödinger devient :
. Ainsi, l'équation de Schrödinger devient :
Cette constante est déterminée encore une fois en testant la solution de l'onde plane où
![]() , et n'est autre que l'énergie de la particule d'où :
, et n'est autre que l'énergie de la particule d'où :
Ces solutions correspondent bien à des états stationnaires car dans ce cas la probabilité de présence de la particule est bien indépendante du temps puisque :
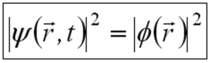
Nous voyons également que l'équation de Schrödinger se réduit à une équation indépendante du temps comme :
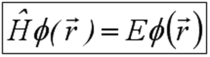
Ces états stationnaires sont d'une grande importance en mécanique quantique, puisqu'ils décrivent l'état d'un système qui n'évolue pas au cours du temps : par exemple un atome dans son état fondamental pour lequel les électrons occupent des états stables dans le temps.
Voir l'animation : Equation de Schöndinger indépendante du temps
Valeurs moyennes
Nous avons vu que la mécanique ondulatoire présente un caractère probabiliste à la base de la théorie quantique. Il est ainsi justifié de définir non pas des grandeurs physiques de façon déterministe comme en physique classique, mais de façon statistique. Nous savons que la valeur moyenne d'une grandeur physique A en statistique s'écrit simplement en fonction de la probabilité P d'apparaître comme :
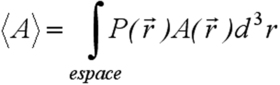
En mécanique ondulatoire, il suffit de remplacer la probabilité par son expression en fonction de la fonction d'onde. Néanmoins, une subtilité apparaît car une grandeur physique en mécanique classique devient un opérateur en mécanique quantique. La valeur moyenne d'une grandeur/opérateur A est alors définie comme :

On voit immédiatement l'importance de cette écriture si on veut obtenir la valeur moyenne de H, qui est un opérateur de dérivée seconde par rapport à la position (pour une particule libre, sans potentiel).
Flux de particules, relations de continuité
Il est également clair qu'une grandeur physique ne peut être décrite par une fonction d'onde discontinue, qui donnerait une probabilité de présence discontinue. La fonction d'onde d'une particule doit donc être continue dans l'espace. Ainsi, si l'espace est séparé en deux régions où par exemple le potentiel vu par la particule est différent, et si la particule se déplace d'une région à l'autre, sa fonction d'onde doit être continue au passage d'un milieu vers l'autre.
Mais il n'y a pas que la fonction d'onde qui doit être continue. Sa dérivée doit l'être aussi et pour justifier ce point, nous nous proposons de formaliser un flux de particule en mécanique ondulatoire. Nous savons en mécanique classique qu'un courant de particule est égal à la densité de particules multipliée par leur vitesse :
Nous savons aussi que la variation temporelle de la densité des particules est liée au gradient du courant qui circule, traduit par la relation de continuité à une dimension :
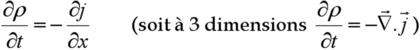
Evidemment, on s'attend à trouver une relation identique en mécanique ondulatoire. Pour la trouver, on identifie naturellement
![]() à la densité de particules et on utilise la relation de Schrödinger de la façon suivante :
à la densité de particules et on utilise la relation de Schrödinger de la façon suivante :
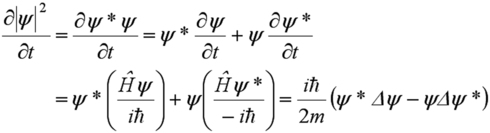
Soit en utilisant la relation
![]() (à 1 dimension) :
(à 1 dimension) :
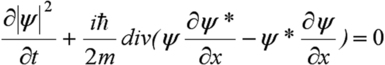
On peut ainsi identifier cette équation à l'équation classique de conservation soit :
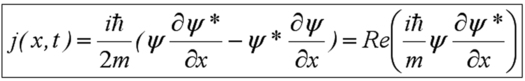
On appelle ainsi j(x,t) la densité de courant de probabilité. Elle sera très utile dans les problèmes que vous aborderez en travaux dirigés. Cette expression montre également que la dérivée de la fonction d'onde doit être continue, puisqu'un courant ne peut être discontinu du point de vue physique (sauf dans le cas très particulier où la fonction d'onde est nulle).