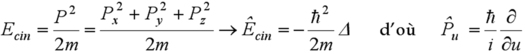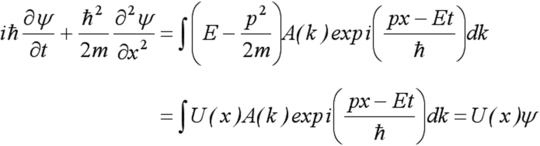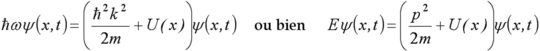1 – Représentation des particules en paquets d'onde
Notion de fonction d'onde
Nous savons qu'un rayonnement peut être décrit par une onde ayant la forme mathématique suivante à 3 dimensions :
où
![]() est l'amplitude de l'onde,
est l'amplitude de l'onde,
![]() le vecteur d'onde, et
le vecteur d'onde, et
![]() la fréquence. Par la suite et pour ne pas alourdir inutilement les notations, nous travaillerons à une dimension dans l'espace, soit :
la fréquence. Par la suite et pour ne pas alourdir inutilement les notations, nous travaillerons à une dimension dans l'espace, soit :
Cette expression qu'on appellera fonction d'onde correspond à une onde non localisée dans l'espace et dans le temps. Dans une expérience de fente d'Young ou de diffraction, les interférences sont obtenues en sommant ces fonctions d'ondes issues des fentes ou des centres diffuseurs. La probabilité de détection du photon sur l'image d'interférence ou de diffraction est ainsi donnée en faisant le module au carré de la somme des fonctions d'onde. Retenons donc que le module carré de la fonction d'onde donne la probabilité de présence de la particule.
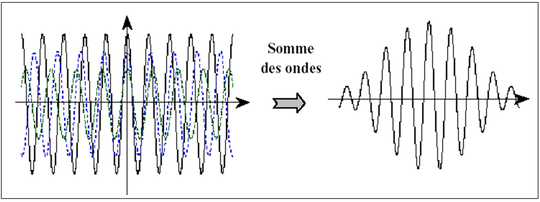
Cet objet mathématique est très utile pour résoudre des problèmes d'optique, mais on s'aperçoit immédiatement que sous cette forme son module carré est le même partout, ce qui veut dire qu'on ne peut localiser et dans le temps et dans l'espace l'onde. A priori, ceci pourrait être compatible avec les photons mais pas avec des particules dites matérielles comme les électrons ou les atomes. Comment s'en sortir mathématiquement ? On sait qu'en sommant quelques ondes de vecteur d'onde (ou de pulsation) proches, on peut alors définir une fonction d'onde non nulle autour de
![]() , et qui s'annulera rapidement lorsqu'on s'éloignera (figure 9). On définit ainsi une onde «localisée» dans l'espace, fabriquée en sommant plusieurs ondes planes dont le vecteur d'onde varie légèrement autour de
, et qui s'annulera rapidement lorsqu'on s'éloignera (figure 9). On définit ainsi une onde «localisée» dans l'espace, fabriquée en sommant plusieurs ondes planes dont le vecteur d'onde varie légèrement autour de
![]() et dont l'amplitude varie d'une onde à l'autre.
et dont l'amplitude varie d'une onde à l'autre.
On parle alors de train d'ondes que l'on écrit sous la forme :
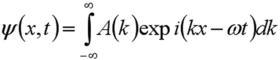
Nous allons ainsi associer cette fonction d'onde localisée dans l'espace à une particule libre de masse
![]() . Comme pour le photon, le module carré de cette fonction donne la probabilité de présence de la particule à l'instant
. Comme pour le photon, le module carré de cette fonction donne la probabilité de présence de la particule à l'instant
![]() et l'abscisse
et l'abscisse
![]() . Ainsi, la probabilité
. Ainsi, la probabilité
![]() de trouver la particule entre
de trouver la particule entre
![]() et
et
![]() est donnée par :
est donnée par :
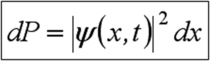
Une conséquence immédiate de ce concept est que la probabilité de présence à chaque instant dans tout l'espace doit être égale à 1, ce que l'on traduit par la relation :
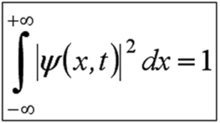
Le lien avec une particule massique n'apparaît pas de façon évidente. Cette ambiguïté peut être néanmoins levée en reprenant les liens établis par Einstein et De Broglie,
![]() et
et
![]() , ce qui donne :
, ce qui donne :
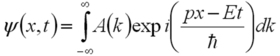
Indétermination sur la mesure
Nous venons de voir qu'une onde plane infinie n'est pas une solution physique appropriée, puisqu'elle est partout à la fois. Ainsi, pour une telle onde, la pulsation (ou le vecteur d'onde) est parfaitement déterminée, mais on ne peut pas dire où est le photon. Il en découle donc une incertitude sur sa position. Cette remarque constitue l'un des fondements de notre nouvelle théorie. Elle apparaît comme une conséquence mathématique des transformées de Fourier lorsqu'on traite une particule comme un paquet d'ondes.
Considérons une fonction quelconque dépendant de la variable
![]() par exemple. Vous verrez en mathématique qu'une fonction peut être décrite comme résultant d'une somme d'ondes planes sinusoïdales telles que :
par exemple. Vous verrez en mathématique qu'une fonction peut être décrite comme résultant d'une somme d'ondes planes sinusoïdales telles que :
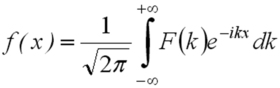
![]() s'appelle la transformée de Fourier de la fonction
s'appelle la transformée de Fourier de la fonction
![]() (En 3 dimensions, il faudra intégrer sur
(En 3 dimensions, il faudra intégrer sur
![]() et et changer la constante en
et et changer la constante en
![]() ), et se calcule par transformée de Fourier inverse à savoir :
), et se calcule par transformée de Fourier inverse à savoir :
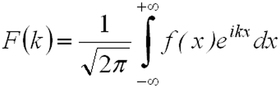
Ainsi, la fonction d'onde définie précédemment n'est autre que la transformée de Fourier de l'amplitude
![]() au signe de k près, elle-même étant la transformée de Fourier inverse de la fonction d'onde (au facteur
au signe de k près, elle-même étant la transformée de Fourier inverse de la fonction d'onde (au facteur
![]() près). Un résultat remarquable du traitement de Fourier est que si la fonction d'onde est normée, alors la transformée de Fourier l'est aussi, c'est à dire :
près). Un résultat remarquable du traitement de Fourier est que si la fonction d'onde est normée, alors la transformée de Fourier l'est aussi, c'est à dire :
Si
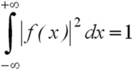 alors
alors
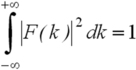
Ceci veut dire tout simplement que si la norme de la fonction
![]() représente la densité de probabilité de présence dans l'espace de la particule, alors la norme de
représente la densité de probabilité de présence dans l'espace de la particule, alors la norme de
![]() représente la densité de probabilité d'avoir un vecteur d'onde
k. Autrement dit, comme
représente la densité de probabilité d'avoir un vecteur d'onde
k. Autrement dit, comme
![]() , elle représente aussi la densité de probabilité de la quantité de mouvement et donc de la vitesse.
, elle représente aussi la densité de probabilité de la quantité de mouvement et donc de la vitesse.
Une autre conséquence directe de ces transformées de Fourier est que plus
![]() est étalée selon
est étalée selon
![]() , plus
, plus
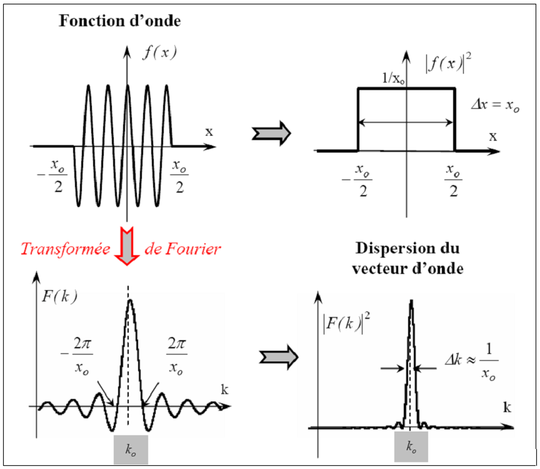
![]() sera au contraire resserrée autour d'une valeur donnée. Autrement dit et pour nous ramener à notre train d'onde, plus le train d'onde est étalé, plus la dispersion en vecteur d'onde est faible. Encore autrement dit, plus la dispersion du vecteur d'onde est faible, moins la particule est localisée. Examinons cela en prenant un exemple simple illustré sur la figure 10. Considérons une fonction d'onde
sera au contraire resserrée autour d'une valeur donnée. Autrement dit et pour nous ramener à notre train d'onde, plus le train d'onde est étalé, plus la dispersion en vecteur d'onde est faible. Encore autrement dit, plus la dispersion du vecteur d'onde est faible, moins la particule est localisée. Examinons cela en prenant un exemple simple illustré sur la figure 10. Considérons une fonction d'onde
![]() définie comme :
définie comme :
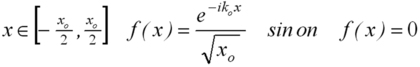
Noter que la fonction est bien normée de telle manière que la probabilité de trouver la particule dans tout l'espace est bien l'unité. La densité de probabilité est ainsi constante dans un intervalle de largeur
![]() , ce qui veut dire qu'on peut trouver la particule en n'importe quel endroit dans cet intervalle. Opérons alors la transformée de Fourier de cette fonction d'onde :
, ce qui veut dire qu'on peut trouver la particule en n'importe quel endroit dans cet intervalle. Opérons alors la transformée de Fourier de cette fonction d'onde :
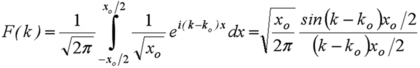
On obtient ainsi une fonction
![]() que vous connaissez et qui présente ici un pic étroit centré sur le vecteur d'onde
que vous connaissez et qui présente ici un pic étroit centré sur le vecteur d'onde
![]() , de largeur à mi-hauteur environ
, de largeur à mi-hauteur environ
![]() . Nous confirmons donc bien que plus
. Nous confirmons donc bien que plus
![]() est petit, plus la particule est localisée, et plus l'incertitude sur le vecteur d'onde est importante.
est petit, plus la particule est localisée, et plus l'incertitude sur le vecteur d'onde est importante.
Le produit
![]() est donc de l'ordre de l'unité et ne peut être nul. Un traitement mathématique plus rigoureux (notamment en définissant correctement les écarts quadratiques moyens
est donc de l'ordre de l'unité et ne peut être nul. Un traitement mathématique plus rigoureux (notamment en définissant correctement les écarts quadratiques moyens
![]() et
et
![]() , que nous verrons par la suite) donne
, que nous verrons par la suite) donne
![]() . Des relations similaires existent évidemment pour les autres coordonnées de l'espace en se plaçant en trois dimensions. Si maintenant on considère le lien entre le vecteur d'onde et la quantité de mouvement selon la relation de De Broglie, ces relations prennent une signification étonnante, puisqu'elles s'écrivent :
. Des relations similaires existent évidemment pour les autres coordonnées de l'espace en se plaçant en trois dimensions. Si maintenant on considère le lien entre le vecteur d'onde et la quantité de mouvement selon la relation de De Broglie, ces relations prennent une signification étonnante, puisqu'elles s'écrivent :
Ainsi, ces relation d'indétermination montrent que si on connaît parfaitement la vitesse de la particule selon
![]() par exemple, alors
par exemple, alors
![]() et donc
et donc
![]() pour satisfaire la relation d'indétermination. Donc on est incapable de localiser la particule dans l'espace. La réciproque est évidemment identique.
pour satisfaire la relation d'indétermination. Donc on est incapable de localiser la particule dans l'espace. La réciproque est évidemment identique.
Voir l'animation : Paquet d'onde et principe d'indétermination
Ces relations sont fondamentales, car elles expriment pleinement la dualité onde – corpuscule : en effet x représente la position, donc l’aspect corpusculaire, et k le vecteur d’onde, donc le caractère ondulatoire. Que dit la relation d’indétermination ? Si vous cherchez à détecter où est la particule, vous préciserez la position, et vous perdrez toute information précise sur le vecteur d’onde. Réciproquement, si vous cherchez à détecter l’onde, par un phénomène d’interférence par exemple, vous précisez le vecteur d’onde, et vous perdrez alors toute chance de localiser précisément la particule. N. Bohr proposait sans démonstration formelle que les expériences pouvaient être décrites soit du point de vue corpusculaire, soit du point de vue ondulatoire, mais pas par les deux voies simultanément. C’est finalement W. Heisenberg qui en apporte l’explication en 1925 par ces relations d’incertitude.
Un raisonnement strictement similaire en considérant cette fois le temps comme variable permet de trouver une relation identique entre la pulsation de l'onde
![]() et la durée du train d'onde T. Pour cela, faisons exactement le même calcul que pour la position. Plaçons nous en une position bien définie x1. A cette position, multiplions l'onde plane par un créneau démarrant à t=0 et se terminant à T. En effectuant un calcul tout à fait similaire au cas précédent pour la position, l'onde résultante peut être décomposée en intégrale (ou série) de Fourier avec une pulsation définie dans une gamme
et la durée du train d'onde T. Pour cela, faisons exactement le même calcul que pour la position. Plaçons nous en une position bien définie x1. A cette position, multiplions l'onde plane par un créneau démarrant à t=0 et se terminant à T. En effectuant un calcul tout à fait similaire au cas précédent pour la position, l'onde résultante peut être décomposée en intégrale (ou série) de Fourier avec une pulsation définie dans une gamme
![]() . On obtient donc une relation d'indétermination en temps et pulsation comme pour la position et la vitesse, à savoir
. On obtient donc une relation d'indétermination en temps et pulsation comme pour la position et la vitesse, à savoir
![]() . Dans le cas général, toujours en définissant plus rigoureusement l'écart quadratique moyen, cette relation s'écrit
. Dans le cas général, toujours en définissant plus rigoureusement l'écart quadratique moyen, cette relation s'écrit
![]() . En raison de la relation d'Einstein entre énergie et pulsation, on trouve donc l'indétermination portant sur l'énergie et le temps :
. En raison de la relation d'Einstein entre énergie et pulsation, on trouve donc l'indétermination portant sur l'énergie et le temps :
Ces relations sur la vitesse et la position d'une part, et sur l'énergie et le temps d'autre part, sont plus souvent connues sous le nom de relations d'incertitude d'Heisenberg :
Conséquence sur la localisation et la durée de vie du train d'onde
Compte tenu des relations sur la vitesse et la position, on pourrait être tenter d'interpréter
![]() comme la taille de la particule. Mais attention, il n'en est rien ! Il faut comprendre ce résultat dans le cadre probabiliste décrit notamment lors de la description de l'expérience des fentes d'Young lorsqu'on envoie les photons un par un. Si on effectue une mesure de la position de la particule, on trouvera une position (avec une certaine incertitude d'après les relations d'Heisenberg) entre-x0/2
et x0/2
avec la probabilité 1/x0 , et il n'y a rien d'autre à dire.
comme la taille de la particule. Mais attention, il n'en est rien ! Il faut comprendre ce résultat dans le cadre probabiliste décrit notamment lors de la description de l'expérience des fentes d'Young lorsqu'on envoie les photons un par un. Si on effectue une mesure de la position de la particule, on trouvera une position (avec une certaine incertitude d'après les relations d'Heisenberg) entre-x0/2
et x0/2
avec la probabilité 1/x0 , et il n'y a rien d'autre à dire.
Prenons l'exemple d'un électron ayant une vitesse de 106 m/s. Admettons que sa vitesse soit connue à 10% près donc
![]() . La masse de l'électron étant égale à 9.10-31 kg, la relation d'Heisenberg conduit à une valeur minimale
. La masse de l'électron étant égale à 9.10-31 kg, la relation d'Heisenberg conduit à une valeur minimale
![]() soit environ 50 000 fois la taille de l'électron (de l'ordre du Fermi soit 10-15 m ). Preuve est faîte de notre propos.
soit environ 50 000 fois la taille de l'électron (de l'ordre du Fermi soit 10-15 m ). Preuve est faîte de notre propos.
Voir l'animation : Localisation et principe d'incertitude d'Heisenberg
Un raisonnement identique peut être fait avec le temps, mais il est possible de préciser la signification de la durée du train d'onde. Pour cela, considérons un système à 2 niveaux d'énergie, et plaçons les particules sur le niveau excité. Afin de minimiser l'état d'énergie du système, les particules vont transiter vers le niveau fondamental. Pour des particules sans interaction, l'équation cinétique bilan conduit à une décroissance exponentielle du nombre de particules sur le niveau excité :
On peut décrire la fonction d'onde des particules dans l'état excité par une fonction d'onde décrivant la position multipliée par une exponentielle temporelle décroissante du type
![]() . Le module carré de la fonction d'onde est donc une exponentielle décroissante dont l'intensité à diminuer de 63% pour
. Le module carré de la fonction d'onde est donc une exponentielle décroissante dont l'intensité à diminuer de 63% pour
![]() et de 82% pour
et de 82% pour
![]() . On définit alors ce temps
. On définit alors ce temps
![]() comme la durée de vie des particules sur le niveau excité. Le traitement temporel de Fourier d'une telle fonction permet de trouver une relation d'incertitude du type
comme la durée de vie des particules sur le niveau excité. Le traitement temporel de Fourier d'une telle fonction permet de trouver une relation d'incertitude du type
![]() . Le niveau d'énergie possède donc une largeur intrinsèque
. Le niveau d'énergie possède donc une largeur intrinsèque
![]() . Ainsi, plus le niveau d'énergie est élevé, plus l'état est instable, et plus la largeur intrinsèque du niveau est grande.
. Ainsi, plus le niveau d'énergie est élevé, plus l'état est instable, et plus la largeur intrinsèque du niveau est grande.
Attention, comme pour la position, ce temps n'est pas la durée de vie de la particule, mais la durée de vie du niveau excité. En effet, la particule n'a pas disparue, elle est sur le niveau fondamental.
Voir l'animation : Localisation et principe d'incertitude d'Heisenberg
Equation d'onde pour les particules
Les particules étant assimilées à des ondes, les scientifiques ont alors cherché à écrire une équation d'onde s'appliquant à ces fonctions d'onde. Pour cela, dérivons d'une part par rapport au temps, et d'autre part par rapport à l'espace la fonction d'onde décrite précédemment. Nous obtenons ainsi :
Or pour une particule dans un potentiel
![]() , et dans le cas non relativiste, on a :
, et dans le cas non relativiste, on a :
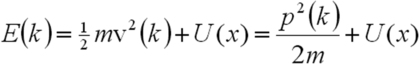
Nous avons rajouté explicitement la dépendance en k pour ne pas faire d'erreur dans l'intégration. En reprenant les deux termes dérivés précédents, et en remarquant que l'intégration s'effectue sur k, on aboutit ainsi à l'équation :
C'est une équation d'onde simple valable dans le cas d'une particule soumis à un potentiel à une dimension :
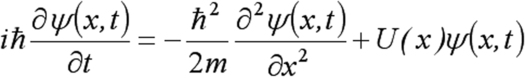
C ‘est la célèbre équation de Schrödinger. Bien sur, ceci ne constitue en rien une démonstration de cette équation. D'autres équations d'onde ont été proposées, mais c'est cette équation qui a permis d'obtenir des résultats en accord avec l'expérience. En outre, ce n'est pas la forme habituelle de l'équation de Schrödinger pour la raison suivante : injectons la solution la plus simple, l'onde plane
![]() , dans l'équation d'onde précédente et on obtient :
, dans l'équation d'onde précédente et on obtient :
Notons que dans l'approche de la mécanique de Hamilton, la quantité « énergie cinétique + énergie potentielle » est appelée Hamiltonien du système, et notée H. En faisant la correspondance entre la grandeur physique H et l'équation aux dérivées partielles, on crée un opérateur noté
![]() :
:
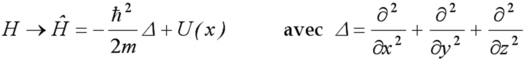
l'équation de Schrödinger s'écrit :
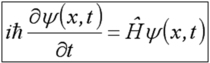
L'hamiltonien apparaît ainsi comme un opérateur agissant sur la fonction d'onde. Il est possible de définir d'autres opérateurs par analogie. Ainsi l'énergie cinétique est définie ici comme un opérateur contenant un laplacien. Comme elle est également définie comme proportionnelle au carré de la quantité de mouvement, on définit ainsi simplement les opérateurs quantité de mouvement
![]() (u=x, y ou z) :
(u=x, y ou z) :