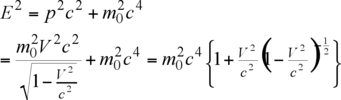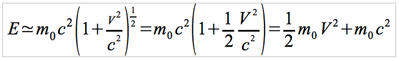Physique Quantique : de la base aux nouvelles technologies
CoursOutils transverses
Relativité et notions de quadrivecteurs
Question
1– donner le quadrivecteur espace-temps et calculer sa norme
Question
2– donner le quadrivecteur impulsion-énergie, calculer sa norme, et donner l’expression de l’énergie en fonction de la quantité de mouvement.
Question
3– Que vaut cette énergie pour des photons ?