2 – Les particules matérielles sont-elles des ondes ?
Introduction : élément de relativité restreinte
Nous voulons dans ce chapitre établir de façon simple des liens entre ce que nous connaissons sur la matière (particule animée d’une quantité de mouvement et possédant une énergie) et ce que nous venons de voir sur les photons (onde avec un vecteur d’onde
et une énergie
). Si on se place dans le cadre de la théorie newtonienne, on se rend compte immédiatement que c’est impossible : l’énergie d’une particule libre alors uniquement cinétique
devient nulle pour un photon puisque sa masse est nulle. D’autre part, on sait que la mécanique newtonienne ne fonctionne plus pour des particules dont la vitesse s’approche de celle de la lumière. Pour aboutir dans notre tâche, il nous faut donc nous placer dans le cadre de la relativité restreinte.
Il ne s'agit pas pour nous ici d'établir de façon complète la relativité restreinte établie par Einstein, mais de donner les idées de base permettant de comprendre les corrections apportées à la mécanique newtonienne. Elle repose sur deux grands principes : la vitesse de la lumière est la même dans tout référentiel et la vitesse d'une particule ne peut dépasser la vitesse de la lumière, quel que soit le référentiel. Encore une notion révolutionnaire d'Einstein : pour que ça " marche ", il faut considérer que le temps n'est pas le même d'un référentiel à l'autre. Il faut donc considérer non plus trois coordonnées d'espace mais ces trois grandeurs plus le temps. On définit ainsi des quadrivecteurs espace-temps
pour un référentiel donné (le temps est transcrit en longueur pour des questions d'homogénéité). En choisissant l'axe
selon la direction de la vitesse relative entre les deux repères, on aboutit à la transformation dite de Lorentz permettant de relier les grandeurs physiques d'un repère à l'autre, à savoir :
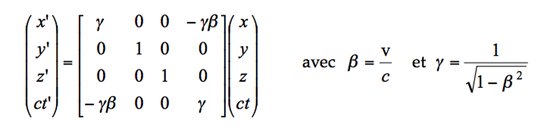
Voir l'animation : Notion de relativité restreinte
On peut alors vérifier qu’avec une telle transformation, les lois physiques ne sont pas changées par un changement de repère galiléen. Par exemple, les forces électromagnétiques doivent avoir la même expression en fonction des champs par changement de repère . Mais cette transformation montre également que le temps n’est pas le même pour deux repères en mouvement l’un par rapport à l’autre. De même les longueurs ne sont pas les mêmes pour deux observateurs dans l’un ou l’autre référentiel. Nous n’allons pas plus loin car ce n’est pas notre propos, mais n’hésitez pas à consulter la littérature sur ce sujet si vous êtes intéressés .
Par contre, nous voulons insister sur un point qui nous sera utile ensuite : dans la théorie de la relativité, on montre que la combinaison des coordonnées du quadrivecteur
ne dépend pas du repère. On peut écrire de façon simple ce résultat en remplaçant la 4ème coordonnée
du quadrivecteur par
et en changeant légèrement la transformation de Lorentz comme :
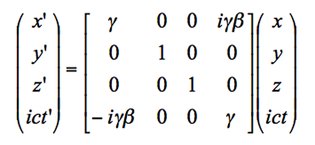
L’invariant précédent est alors la norme du quadrivecteur. Dans cette théorie, les quadrivecteurs sont ainsi définis de telle manière que leur norme ne dépend pas du repère choisi.
Einstein étend ces notions à la dynamique. On sait effectivement que lors d'une collision entre deux particules, la quantité de mouvement est conservée. Tout l'exercice est donc de trouver la bonne expression de la quantité de mouvement telle que ce principe reste vrai si on le regarde dans deux référentiels différents. Il suffit en fait de continuer à garder l'expression
mais il faut reconsidérer la masse en l'écrivant sous la forme :
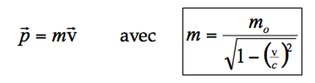
où
est la masse au repos de la particule. La relation fondamentale de la dynamique et l’énergie de la particule deviennent alors:
Le quadrivecteur impulsion et par suite l’invariant s’écrivent alors :
et cette constante peut être facilement déterminée puisque, pour un repère dans lequel la particule est au repos, on a alors
,
d’où :
donc :
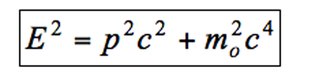
Il est alors possible de construire un quadrivecteur impulsion qui obéit à la transformation de Lorentz, à savoir
. La transformation s’écrit ainsi pour un déplacement du repère selon l’axe x à la vitesse
:
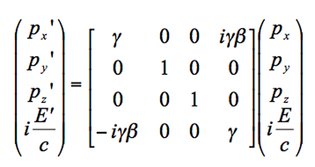
Terminons sur une remarque d'importance, en examinant ce que devient cette expression pour des vitesses faibles. Un calcul trivial de développement limité donne :
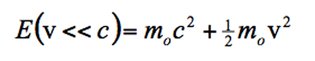
On reconnaît donc l'énergie cinétique, mais l'énergie totale contient aussi l'énergie au repos. Cette énergie (très grande : 0,511 MeV pour l'électron, environ 940 MeV pour le proton et le neutron) n'est pas prise en compte en mécanique classique. Ce n'est pas faux car l'énergie est définie à une constante près, sauf en physique des particules, lorsqu'il y a annihilation ou création de particules.
L'hypothèse de De Broglie
Soyons avant tout précis : nous parlons ici de particules ayant une masse, au contraire des photons qui ont une masse nulle. Nous venons donc de voir qu’un photon est à la fois une onde et un corpuscule. De Broglie (prononcez " De Breuil ") a sauté le pas au cours de sa thèse en 1923, en proposant d’associer aux particules matérielles une longueur d’onde telle que :
Allons un peu plus loin dans son approche. Si une onde doit être associée à une particule ayant une trajectoire par exemple selon l’axe
, on doit écrire cette onde sous la forme :
Notre but est d’essayer de relier les grandeurs caractéristiques
et
de l'onde à celles associées habituellement à la particule, à savoir
,
(ou
), et
.
L'onde précédente est une onde plane, dont la vitesse de groupe
peut être associée à la vitesse de la particule. Cette vitesse de groupe est alors reliée à la quantité de mouvement donnée par la relativité restreinte, soit :
Mais il nous faut une autre hypothèse pour justifier l’expression de De Broglie. Supposons que l’expression de l’énergie introduite pour les photons reste valable pour les particules. On a ainsi le lien entre l’énergie d’une particule ayant une masse (en relativité restreinte) et le quantum d’énergie tel que:
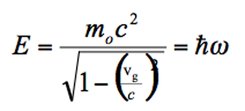
En remplaçant la vitesse de groupe par
et en séparant les variables, on obtient :
L'intégration n'est pas difficile. La constante d'intégration s'obtient en remarquant que
pour
et dans ce cas
d'où :
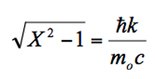
et en remarquant que
, on obtient ainsi
Le modèle de Bohr justifié
L'approche de De Broglie permet en fait de justifier l'hypothèse de Bohr. En effet, Bohr proposait de quantifier le moment cinétique, hypothèse totalement arbitraire à cette époque. De Broglie propose alors que la longueur d'onde associée à l'électron soit un multiple de la distance parcourue sur l'orbite. Ce raisonnement n'était pas parachuté, car les physiciens de l'époque savaient déjà quantifier le rayonnement dans une cavité : le raisonnement était basé sur le fait que l'onde incidente et l'onde réfléchie doivent être en phase conduisant à des ondes stationnaires (raisonnement suivi au début de ce cours pour le rayonnement du corps noir). Ainsi, pour que l'onde décrite par l'électron ne se détruise pas en se refermant sur une orbite circulaire de rayon
, on doit avoir :
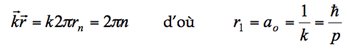
et en appliquant la relation fondamentale de la dynamique comme nous l’avons fait dans la première partie, on retrouve l’expression du rayon de Bohr. L’hypothèse de De Broglie permet donc de justifier la quantification proposée par Bohr. Néanmoins, ce modèle n’est pas totalement satisfaisant en raison de l’hypothèse simpliste de la trajectoire circulaire. Mais cette hypothèse est aussi en accord avec l’aspect corpusculaire du photon proposé par Einstein. En effet, si nous écrivons l’énergie relativiste pour une particule sans masse comme le photon, on obtient en utilisant la relation de De Broglie :
L'hypothèse de De Broglie donne donc une vision cohérente et unifiée de la dualité onde-corpuscule (matière-rayonnement).
Mais alors, les particules peuvent diffracter ?
Pour vérifier si De Broglie avait raison, rien de plus " simple " : il suffit de réaliser une expérience de type fentes d’Young mais avec des particules. Malheureusement, il y a un petit problème. En effet, l’expérience des fentes d’Young est réalisable techniquement sans trop de difficulté pour des photons dans le visible, c’est à dire avec une longueur d’onde de l’ordre du µm. Peut-on facilement obtenir des particules avec une telle longueur d’onde. L’expression précédente montre que la longueur d’onde sera d’autant plus grande que la masse est petite. Choisissons donc un électron. Un bon moyen d’émettre des électrons est de chauffer (2500K) un filament de tungstène jusqu’à émission spontanée d’électrons. En considérant que l’électron sort avec l’énergie thermique
par degré de liberté, on peut alors estimer la longueur d’onde, en négligeant les effets relativistes (hypothèse justifiée, calculez la vitesse) :
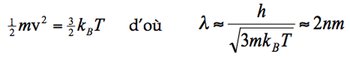
On obtient donc une longueur d’onde extrêmement petite ! Il était donc impossible à l’époque de réaliser une expérience de type fente d’Young avec des particules. Par contre, on savait que la distance entre les atomes dans la matière est de l’ordre de 0,2-0,4 nm. Il suffit ainsi d’envoyer un faisceau de particules ayant une telle longueur d’onde sur un échantillon où les atomes sont parfaitement ordonnés (on parle alors de monocristal) pour voir des franges de diffraction, ou plus exactement des directions privilégiées de l’espace pour lesquelles les corpuscules associés à des ondes interfèrent de façon constructive : c’est la diffraction. Chaque atome joue le rôle d’un trou d’Young, en diffusant l’onde incidente, comme pour un réseau diffusant un faisceau lumineux monochromatique. Davisson et Germer dans leur célèbre expérience de 1927 observèrent pour la première fois la diffraction vers l’arrière d’un monocristal de nickel, démontrant ainsi le caractère ondulatoire des électrons (figure 7).
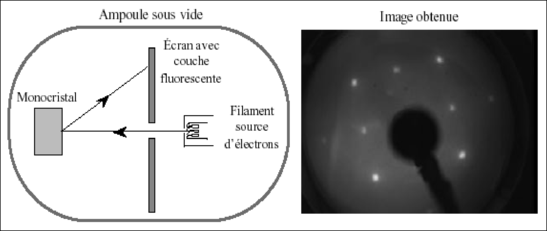
Figure 7 : à gauche, schéma de l’expérience de Davisson et Germer. Ce type d’appareillage est maintenant utilisé pour étudier les surfaces monocristallines. On parle de LEED (Low Energy Electron Diffraction). Une image LEED obtenue sur un réseau carré est donnée à droite
Par la suite, des expériences de diffraction ont été démontrées avec d’autres particules ayant une masse comme les neutrons par exemple. Des réacteurs nucléaires sont d’ailleurs spécialement dédiés à la production de neutrons froids pour les études de la matière par diffraction de neutrons. Plus récemment, l’aspect ondulatoire des atomes a même pu être mis en évidence en utilisant des atomes ultra-froids. Ces expériences de diffraction sont également possibles en utilisant un rayonnement, mais il faut alors que la longueur d’onde soit petite, inférieure au nanomètre. Il s’avère que Röntgen a découvert un rayonnement particulier de très faible longueur d’onde qu’il a appelé rayons X. Ce rayonnement n’est en fait pas " nouveau " en ce sens qu’il est constitué de photons. Simplement, ces photons ne sont pas visibles à l’œil nu. La diffraction de rayons X est une technique largement utilisée pour caractériser la matière, tout simplement parce qu’elle ne nécessite pas de travailler sous vide comme avec des électrons, et qu’ils sont faciles à obtenir par simple transition électronique entre deux niveaux d’énergie.
