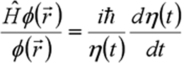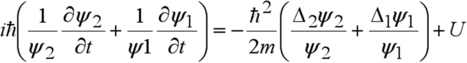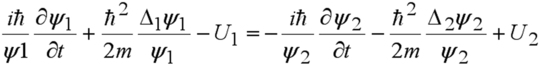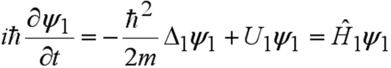Les particules étant indépendantes, on peut séparer les variables dans la fonction d'onde soit :
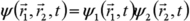 . En l'injectant dans l'équation de Schrödinger on obtient :
. En l'injectant dans l'équation de Schrödinger on obtient :
Les indices sur les laplaciens indiquent le type de coordonnées sur lesquelles s'effectue la dérivation. En divisant par la fonction d'onde totale, on isole les variables dans l'équation :
Il convient de considérer la forme de l'énergie potentielle U. Les particules étant indépendantes, on peut séparer cette énergie en deux termes, l'une dépendant de
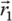 , l'autre de
, l'autre de
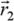 :
:
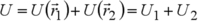 . L'équation précédente peut ainsi s'écrire comme :
. L'équation précédente peut ainsi s'écrire comme :
La séparation des variables est bien effectuée, les deux termes sont donc constants et on aboutit en prenant cette constante nulle (l'énergie est défini à une constante près) à deux équations de Schrödinger pour chaque particule :
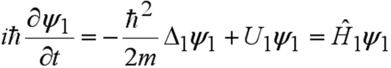 et idem pour
et idem pour
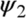
On remarque également que l'hamiltonien total s'écrit en fonction des hamiltoniens individuels :
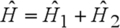 , et donc que l'énergie totale est bien la somme des énergies individuelles
, et donc que l'énergie totale est bien la somme des énergies individuelles
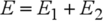 .
.
Attention :
Il convient de faire une remarque importante. U1 et U2 ne sont pas les potentiels pour la particule seule.
La situation est plus complexe, prenons l'exemple de 2 atomes d'hydrogène, ou l'on cherche les fonctions d'onde du système des 2 électrons considérés indépendants, c'est-à-dire qu'on néglige la répulsion coulombienne entre eux. U1 est donc l'énergie potentielle de l'électron 1 dans le potentiel du noyau 1 additionné de l'énergie potentielle de cet électron dans le potentiel du noyau 2.
![]() . Montrer que l'équation de Schrödinger appliquée à cette fonction peut se décomposer en 2 équations, l'une agissant sur
. Montrer que l'équation de Schrödinger appliquée à cette fonction peut se décomposer en 2 équations, l'une agissant sur
![]() , l'autre sur
, l'autre sur
![]() . En déduire l'expression de l'énergie totale E en fonction de l'énergie de chaque particule.
. En déduire l'expression de l'énergie totale E en fonction de l'énergie de chaque particule.