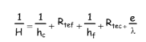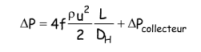Calcul des coefficients de transfert de chaleur
4.1. Coefficient de film
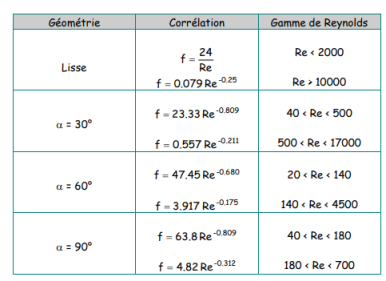
Les corrélations proposées pour calculer le coefficient de film de transfert de chaleur dépendent principalement de la géométrie des plaques et notamment de l’angle de corrugation α, défini sur la figure 10 ci-dessous.
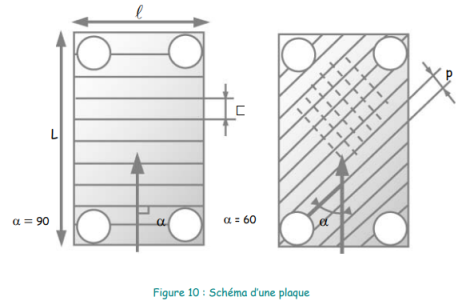
• α est l’angle de corrugation, formé par la direction principale de l’écoulement et la direction des corrugations (α = 90° pour des plaques à cannelures droites et α < 90° pour des plaques en chevrons)
• p est le pas de corrugation (distance entre deux motifs identiques),
• dplaques est la hauteur de corrugation, ou hauteur du canal, ou distance entre deux plaques
• L est la hauteur de la plaque,
• l (soit petit L) est la largeur de la plaque.
Les expressions donnant le coefficient de film sont alors de la forme :
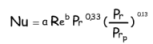
où :
- Nu est le nombre de Nusselt, défini par :
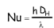
- Re est le nombre de Reynolds défini par :
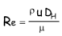
- Pr est le nombre de Prandtl, défini par :
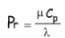
- DH est le diamètre hydraulique, défini par :
Soit ici :
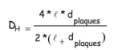
Où dplaques est la distance entre deux plaques,
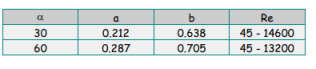
Enfin, a et b varient en fonction de l’angle de corrugation α :
4.2. Perte de charge
La perte de charge dans l’installation est calculée par la corrélation suivante :
où collecteur ∆P est souvent négligeable.
Le problème se ramène alors au calcul du coefficient de frottement f.
On se référera au tableau suivant :
4.3. Coefficient global de transfert de chaleur
Le coefficient global d’échange de chaleur est alors calculé par :
