Contraintes

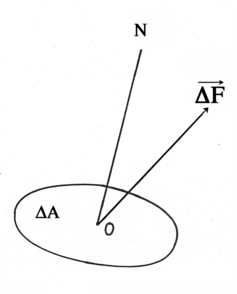Figure 1

Soit un solide en équilibre sous l'action de forces internes et externes. Si on le coupe en deux parties, il faut appliquer des forces sur la section de la partie restante pour maintenir l'équilibre. Soit un petit élément de surface ΔA de cette section. et la force qui lui est appliquée. Le vecteur contrainte au point O, relatif à la face ΔA dont la normale est N se définit de la façon suivante :

Ceci entraîne :

1 - La contrainte a les dimensions d'une pression (force/ surface)

2 - Elle est définie en un point pour une section donnée

3 - Elle a une orientation quelconque par rapport à la section

4 - Comme en un point l'on peut définir une infinité de sections, il y a donc une infinité de vecteurs contrainte en ce point

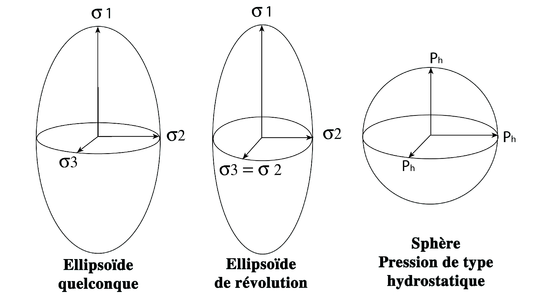
On parle alors de l'état des contraintes en un point. Cet ensemble des vecteurs peut se décrire par un tenseur ou se représenter sous la forme d'un ellipsoïde dont les axes principaux sont appelés contraintes principales majeure, moyenne et mineure.

L'ensemble des états de contrainte dans un domaine donné définit le « champ de contraintes » régnant dans ce domaine et permet de tracer des trajectoires de contraintes.

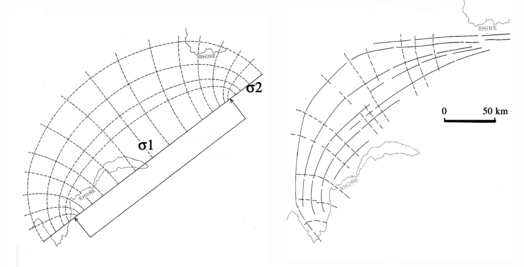
Ci-dessus modèle idéal de trajectoires de contraintes développées par un piston sur un demi-plan élastique (en contraintes planes) comparé à des trajectoires déduites des axes de plis et des décrochements dans la chaîne du Jura (Laubscher, 1972).

.