3 – L'émission stimulée : une nouveauté quantique
La découverte de l'émission stimulée par Einstein
A. Einstein, encore lui, découvre un phénomène tout à fait particulier en examinant l’absorption et l’émission de photon par un gaz de particules à l’équilibre. Son objectif dans cette approche formelle est d’appliquer la théorie des gaz à l’équilibre de Maxwell-Boltzmann d’une part, et les équations cinétiques d’absorption et d’émission d’autre part, afin d’en examiner la cohérence. A l’équilibre thermodynamique, il convient de considérer d’une part le gaz de particules, régit par la statistique de Maxwell – Boltzmann, et le rayonnement électromagnétique ou les photons, régit par la loi du rayonnement du corps noir. L’approche cinétique permet d’établir les échanges entre le gaz de particules, et le rayonnement, par les phénomènes d’absorption et d’émission. Le lien entre ces deux approches thermodynamique et cinétique est fondée sur le fait que le régime cinétique, une fois la phase transitoire atteinte et donc le régime permanent atteint, doit donner des résultats en accord avec l’équilibre thermodynamique. Il convient donc que toutes ces approches soient cohérentes, et c’est ce qu’Einstein se propose d’examiner. Le milieu considéré est un gaz de particules sans interaction. Chaque particule peut exister sous deux états d’énergie : un état stable d’énergie E1 et un état excité d’énergie E2. Chaque particule peut passer d’un état à un autre en absorbant ou bien en émettant un photon, selon le modèle de Bohr. Considérons tout d’abord l’aspect thermodynamique appliqué au gaz de particules sans interactions. La théorie des gaz de Maxwell- Boltzmann stipule dans ce cas que les densités de population des particules dans les états E1 et E2, notées N1 et N2, sont reliées entre elles à la température par la relation que vous connaissez :
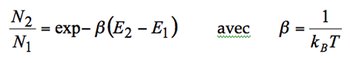
L’équilibre thermodynamique pour le rayonnement électromagnétique conduit à la densité d’énergie donnée par la loi de Planck, à savoir :
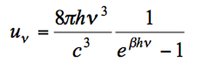
Ecrivons maintenant les équations cinétiques régissant les populations de particules dans les états 1 et 2. Une équation cinétique en physique s’écrit simplement en faisant le bilan suivant :
Ecrivons cela pour le niveau E2 par exemple. Les particules étant sans interaction, si une particule quitte un niveau vers un autre, elle n'affecte en rien la probabilité des autres particules de passer d'un niveau à l'autre. Autrement dit les probabilités de transition ne dépendent pas du nombre de particules. Ainsi, le flux de particules qui part vers le niveau fondamental est proportionnel à la probabilité de passer de E2 à E1, notée A, fois le nombre de particules sur le niveau excité, soit :
Pour ce qui arrive, il faut considérer que le rayonnement électromagnétique est nécessaire. Une particule ne passe sur un niveau excité que si elle absorbe un photon. La probabilité de transition est donc proportionnelle à la densité d’énergie électromagnétique
![]() et à la densité de particules sur l’état fondamental, soit :
et à la densité de particules sur l’état fondamental, soit :
Notez bien que les constantes A et B, appelées constantes d’Einstein, ne dépendent ni des nombres de particules, ni de la densité de photon. L’équation cinétique bilan s’écrit donc comme :
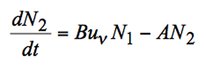
Voir l'animation : Cadre du modèle d'Einstein
En régime permanent, les flux arrivant et sortant se compensent, et on obtient ainsi le rapport des populations comme :
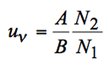
Le lien avec la thermodynamique s’effectue à ce stade. On connaît ce rapport, il est donné par la statistique de Maxwell – Boltzmann. On en déduit donc l’expression de la densité d’énergie électromagnétique, sachant que l’absorption ou l’émission nécessitent la création ou l’annihilation d’un photon d’énergie
![]() selon le modèle de Bohr, soit :
selon le modèle de Bohr, soit :
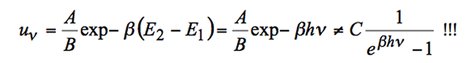
Or cette densité d’énergie est aussi donnée par la loi du rayonnement du corps noir. Force est de constater que si le résultat cinétique est en accord avec la loi de Planck à basse température, il n’en est rien sur toute la gamme de température. A. Einstein met donc le doigt sur une incohérence flagrante. Comment régler ce problème ? A. Einstein propose une méthode extrêmement simple : il convient de chercher ce qu’il faut rajouter dans l’équation cinétique afin de rendre tout cohérent :
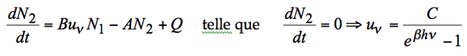
Une fois l’expression mathématique nécessaire trouvée, nous réfléchirons comme Einstein à sa signification. Faîtes cet exercice, et vous trouverez qu’il faut écrire :
Que signifie ce terme ? Tout d’abord il est négatif, ce qui correspond à une perte de population sur le niveau excité. Il est proportionnel à N2 ce qui est cohérent avec ce flux provenant de l’état excité. Mais chose étrange, il est aussi proportionnel à la densité d’énergie ! Il est donc provoqué par l’interaction avec un photon, contrairement à l’émission spontanée d’un photon par simple désexcitation liée à la température. On parle alors d’émission stimulée, car stimulée par le rayonnement électromagnétique, à distinguer de l’émission spontanée ne nécessitant pas de photon. A. Einstein complète donc le modèle de Bohr en rajoutant le mécanisme d’émission stimulée, dont la figure suivante fait un bilan :
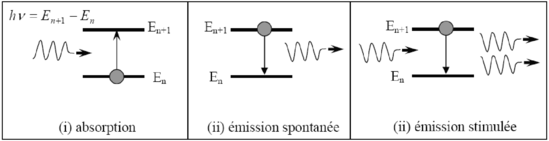
Voir l'animation : Modèle de Bohr complété
Rien en physique classique, ni même avec les prémisses de la physique quantique, ne permet de justifier un tel résultat. Nous verrons que ce mécanisme découlera directement du formalisme final de la physique quantique sans qu’on ait besoin de rajouter d’autres hypothèses. Il est étonnant qu’Einstein ait découvert ce processus, alors que non seulement il ne travaillait pas directement sur l’établissement de la théorie quantique, mais en plus il était extrêmement critique sur son interprétation (mais pas sur sa validité expérimentale).
LASER à photons, LASER à électrons
Cette découverte de l’émission stimulée aura des conséquences importantes pour les applications, mais bien plus tard. En effet, un fait remarquable de ce mécanisme est que les deux photons présents après le processus sont rigoureusement identiques : ils ont la même fréquence, et la même quantité de mouvement en valeur absolue. On dit qu’ils sont cohérents. Il serait donc possible de fabriquer à partir de ce principe une source de photons cohérents très intense émettant dans une direction très précise. Pour arriver à une telle réalisation, on peut cependant montrer (voir les exercices) qu’il faut inverser la population entre les niveaux fondamental et excité, c'est-à-dire que le nombre de photons sur l’état excité soit plus grand que le nombre de photons sur l’état fondamental en régime permanent. Pour un système à deux niveaux, c’est impossible en raison de la thermodynamique, la statistique de Maxwell – Boltzmann montrant qu’au mieux on peut égaler les populations. Il a donc fallu attendre 1960 pour trouver un moyen d’inverser cette population en recourant à des systèmes plus complexes avec plus de deux niveaux impliqués (voir exercices). Un tel appareil fonctionnant avec des photons s’appelle un LASER, pour Light Amplifier by Stimulated Emission of Radiation. Dans un laser, en plus de l’émission stimulée, on utilise les interférences constructives du rayonnement émis pour fabriquer une onde monochromatique très intense. Pour cela, on emprisonne un gaz entre deux miroirs, l’un étant totalement réfléchissant, l’autre partiellement. Ce gaz étant chauffé émet des photons qui se propagent entre les deux miroirs. Seuls les modes tels que les interférences soient constructives entre l’onde incidente et l’onde réfléchie se propagent, ce qui permet d’obtenir un rayonnement monochromatique avec une dispersion en longueur d’onde extrêmement faible. Pour cette raison, le LASER est souvent utilisé pour mener à bien des travaux pratiques d’interférence. Compte tenu de la dualité onde-corpuscule, il n’y a donc aucune raison de ne pas obtenir un faisceau LASER à partir de particules matérielles. Depuis une trentaine d’années, on utilise des dispositifs appelés synchrotron : ce sont des accélérateurs de particules, des électrons ou des positrons, qui permettent d’obtenir des rayons X par simple déviation des électrons (positrons) dans un champ magnétique. Ceux-ci émettent alors un rayonnement dit blanc de longueur d’onde dans le domaine des rayons X (de l’ordre du nm). Grâce à ces accélérateurs, on est capable de fabriquer des lasers à électrons, appelés LASER à électrons libres, qui permettent d’obtenir un faisceau d’électrons d’une très grande intensité et très monochromatique. Dans ce genre de dispositif, l’aspect ondulatoire de l’électron est, s’il le fallait encore une fois, clairement établi.
